3) При возведении обеих частей уравнения в одинаковую четную степень не всегда получаются равносильные уравнения.
Пошаговое объяснение:
1) Утверждение не верно.
Иррациональными называются уравнения, в которых переменная содержится под знаком корня. Например:
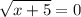
Это уравнение имеет корень х = -5!
2) Утверждение не верно.
Например, если возвести в нулевой степень (0 принадлежит множеству действительных чисел) уравнение, имеющий только корень х=0:
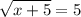
то получим
1 ≡ 1, что означает, последнее верно для любого х∈R.
3) Утверждение верно.
Уравнения называются равносильными, если имеют одно и то же множество корней.
В самом деле, рассмотрим иррациональное уравнение, которое не имеет корней:
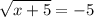
После возведения в квадрат получим:
x+5=25
А это уравнение имеет корень x=20!
S - расстояние v - скорость t - время
ГЛАВНАЯ ФОРМУЛА: S = v * t
расстояние = скорость * время
v = S : t - скорость = расстояние : время
t = S : v - время = расстояние : скорость
S = t * v сб.
расстояние = время * скорость сближение
ВСТРЕЧНОЕ ДВИЖЕНИЕ:
v сб. = v₁ + v₂ ( скорость сближения = сумме скоростей)
ДВИЖЕНИЕ ВДОГОНКУ:
v сб = v₁ - v₂ ( скорость сближения = разности скоростей)
S = t * v уд.
расстояние = время * скорость удаления
ДВИЖЕНИЕ В ПРОТИВОПОЛОЖНЫХ НАПРАВЛЕНИЯХ:
v уд. = v₁ + v₂ ( скорость удаления = сумме скоростей)
ДВИЖЕНИЕ С ОТСТАВАНИЕМ:
v уд. = v₁ - v₂ ( скорость удаление = разности скоростей)