По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
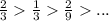
По второму признаку Лейбница предел ряда должен стремится к 0.
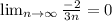
Второе условие Лейбница выполняется. Таким образом, ряд сходится. Исследуем теперь ряд на абсолютной и условной сходимости. Для этого рассмотрим данный ряд по модулю
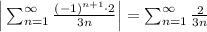
Этот ряд расходится, так как это гармонический ряд и он является расходящимся.
Таким образом, данный исследуемый ряд сходится условно.
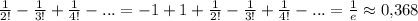
Пошаговое объяснение:
здесь главное не перепутать экстремумы и максимальное и минимальное значение функции и соответственно точки, где эти экстремумы есть а где функция достигает наибольшего и наименьшего значения.
Точка максимума (или минимума) — это внутренняя точка ООФ, где значение функции больше (или меньше), чем во всех достаточно близких к ней точках. т.е. это локальный пик графика
у нас экстремумы - это точки
х = 1 -1 -3 -5 -6 - это все локальные пики.
теперь понятно, что
локальные максимумы - это точки х = -1 и х = -5