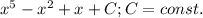
Пошаговое объяснение:
Для того, чтобы найти все первообразные функции 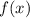 , требуется найти неопределенный интеграл от этой функции
, требуется найти неопределенный интеграл от этой функции 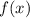 .
.
Нам дана функция: 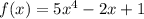 .
.
Формула нахождения неопределенного интеграла имеет вид:
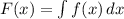
Подставим нашу функцию в формулу выше:
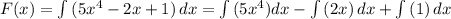
Теперь каждый найдем неопределенный интеграл по отдельности
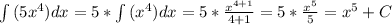
Данный интеграл находится используя свойство интегралов:
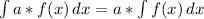
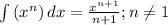
Далее найдем второй интеграл:
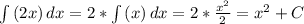
Используем аналогичные свойства интегралов, что и выше.
И последний интеграл от 1:
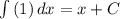 , где C - константа интегрирования.
, где C - константа интегрирования.
Все вместе будет иметь вид:
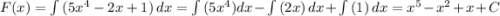 - это и будет ответ.
- это и будет ответ.