![x_{2}=- \frac{1}{ \sqrt[3]{1+ \sqrt{2} } }+ \sqrt[3]{1+ \sqrt{2} }](/tpl/images/0848/5929/cd322.png)
Пошаговое объяснение:
f(x)=х³-6х²+5
точки экстремума определяются по первой производной
f'(x)(x₀) = 0 - это необходимое условие экстремума функции
получим промежутки монотонности
если на промежутке f′(x)<0, то на этом промежутке функция убывает;
если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
Если в окрестности критической точки f′(x) меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
решение
f'(x)=(х³)'-6(х²)' +5 = 3x² -12x +0
3x² -12x = 0; 3x(x - 4) =0; x₁ = 0; x₂= 4 - это и есть точки экстремума
промежутки монотонности функции
(-∞ ;0) (0; 4) (4; +∞)
теперь на каждом промежутке определим знак производной. для этого возьмем любую точку возле точки экстремума, принадлежащую промежутку, и посмотрим на знак производной в этой точке
(-∞ ;0) х = -1; f'(-1) = 15 > 0, функция возрастает
(0; 4) x = 1; f'(1) = -9 <0, функция убывает
(4; +∞) x = 5 f'(5) = 12> 0, функция возрастает
вот, в общем-то, и все.
можно дополнительно сказать, что
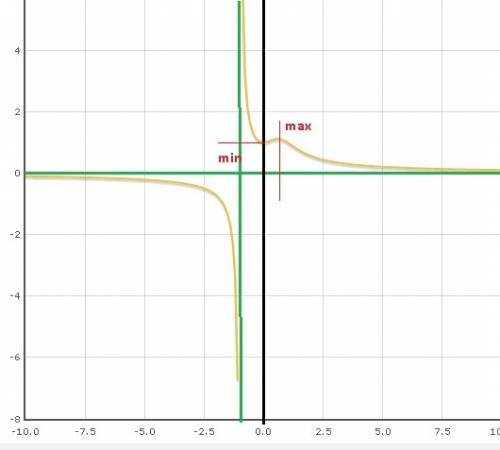
в окрестности точки x = 0 производная функции меняет знак с (+) на (-), значит, точка x = 0 - точка максимума.
в окрестности точки x = 4 производная функции меняет знак с (-) на (+), значит, точка x = 4 - точка минимума.