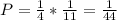
В момент детонации «Малыша»
двухлетняя Садако была дома.
Взрывная волна вынесла её через
окно, но девочка осталась жива. Когда
мать нашла её, она не заметила у
дочери каких-либо видимых травм.
До 1954 года Садако росла обычной
девочкой и даже была членом
эстафетной команды класса. В ноябре
1954 года у неё проявились первые
признаки болезни - на шее и позади
ушей проявилась опухоль.
В январе 1955 года опухоль появилас:
на ногах, и 20 февраля девочка была
госпитализирована с диагнозом
лейкемия. По мнению докторов, ей
оставалось жить не больше года. 21
февраля её перевели в хиросимскую
больницу Красного Креста для лечени
и переливания крови. Ктому времени
уровень лейкоцитов в её крови был
в шесть раз выше по сравнению со
средним уровнем обычного ребёнка.
В августе 1955 года она переехала
в палату, где её соседкой оказалась
Киё, всего на два года старше. Вскоре
друзья Киё принесли ей бумажных
журавликов. Отец Садако, Сигэо, узна
от дочери о журавликах, рассказал ей
легенду, согласно которой человек,
сложивший тысячу бумажных
журавликов, может загадать желание,
которое обязательно исполнится.
Легенда впечатлила Садако, и она,
как многие другие пациенты, стала
складывать журавликов из любых
попадавших в её руки кусочков
бумаги. Её подруга Тидзуко Хамамото
приносила ей для этого кучу бумаги из
школы.
Междутем здоровье Садако
постепенно ухудшалось. Примерно в
середине октября левая нога распухла
и приобрела фиолетовый цвет. После
того, как семья уговорила её поесть,
Садако попросила чай с рисом. Затем
она поблагодарила семью, и это были
её последние слова. 25 октября 1955
года девочка умерла в возрасте 12 лет
По легенде из книги «Садако и
тысяча бумажных журавликов», она
успела сделать лишь 644 журавлика.
Её друзья якобы закончили работу,
и Садако была похоронена вместе
с тысячей бумажных журавликов.
Однако на выставке, посвящённой
Садако в Мемориальном музее мира
Хиросимы, приводится информация
о том, что девочка успела смастерить
около 1300 бумажных журавликов.тысяча бумажных журавликов», она
успела сделать лишь 644 журавлика.
Её друзья якобы закончили работу,
и Садако была похоронена вместе
с тысячей бумажных журавликов.
Однако на выставке, посвящённой
Садако в Мемориальном музее мира
Хиросимы, приводится информация
о том, что девочка успела смастерить
около 1300 бумажных журавликов.
Брат Садако, Масахиро, в своей книге
«Полная история Садако Сасаки» тоже
подтвердил, что сестра на момент
смерти уже успела сложить заветную
тысячу журавликов.