Обозначим этот определитель через  Раскладывая его по первой строке, получаем
Раскладывая его по первой строке, получаем

(последнее равенство получено с разложения по первому столбцу). Конечно, в этом равенстве предполагается, что n>2.
Непосредственно ищем 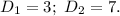 используя выведенную формулу, находим
используя выведенную формулу, находим 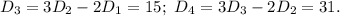 Замечаем такую закономерность:
Замечаем такую закономерность:
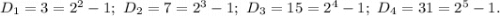
Естественно возникает гипотеза, что для любого натурального n

Докажем это. Для начальных значений n гипотеза уже проверена, остается проверить индукционный переход. А именно, предположив, что гипотеза верна при n=k и n=k+1, докажем, что тогда она верна и при n=k+2. В самом деле,


Тем самым гипотеза доказана при всех натуральных n.
Замечание. Задачу можно было бы решить с характеристического уравнения, но в этом случае пришлось бы слишком много объяснять.
ответ: 
решение примеров:
пример №1.
632702: 7+303804: 6-882910: 7=14890
1. первое действие делаем деление.
632702/7=90386;
2. второе действие делаем деление.
303804/6=50634;
3. третье действие делаем деление.
882910/7=126130;
4. четвертое действие делаем сложение.
90386+50634=141020;
5. пятое действие делаем вычитание.
141020-126130=14890.
пример №2.
(240238: 8+654084+20): 7=97733,392
1. первое действие делаем в скобках деление.
240238/8=30029,75;
2. второе действие в скобках сложение.
30029,75+654084+20=684133,75;
3. третье действие делаем деление.
684133,75/7=97733,392.
пример №3.
(2118*105: 3-654084: 9)*607=882578
1. первое действие делаем в скобках умножение и деление.
2118*105/3=74130
2. второе действие делаем деление в скобках.
654084/9=72676;
3. третье действие делаем вычитание в скобках.
74130-72676=1454;
4. четвертое действие делаем умножение.
1454*607=882578.
Дальше я буду упрощать наше уравнение до тех пор, пока не получу уравнение кривой на плоскости.
Последнее уравнение - это уравнение серединного перпендикуляра к отрезку