1.задание
1) 48, 051
2) 54290
3) 0,378
4) 0,25
5) 1,15
6) 20
2.задание
50 - (22,95 : 2,7 + 3,4) * 2,8 = 16,68
1) 22,95 : 2,7 = 8,5
2) 8,5 + 3,4 = 11,9
3) 11,9 * 2,8 = 33,32
4) 50 - 33,32 = 16,68
3.задание
0,144:(3,4-х)=2,4
3,4-х=0,144:2,4
3,4-х-=0,06
х=3,4-0,06
х=3,34
4.задание
58,4*4=233,6 км проехал первый поезд
233,6+25,6=259,2 км проехал второй поезд
259,2/4=64,8 км/ч скорость второго поезда
5.задание
Обозначим через х искомую десятичную дробь.
Если в любой десятичной дроби перенести запятую вправо на одну цифру, то это равносильно умножению данной дроби на 10.
Согласно условию задачи, после переноса в данной десятичной дроби запятой на одну цифру вправо, данная дробь увеличилась на 44.46, следовательно, справедливо следующее соотношение:
10*х = х + 44.46.
Решаем полученное уравнение:
10*х - х = 44.46;
9*х = 44.46;
х = 44.46/9;
х = 4.94.
ответ: искомая десятичная дробь 4.94.
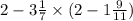
Сначала для удобства переведём дроби в неправильные:
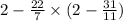
Теперь поочерёдно начнём выполнять действия. Первым действием является скобка. Перед тем, как выполнить вычитание, нужно привести оба числа в одинаковому знаменателю, для этого умножим 2 на 11 и после этого вычтем:
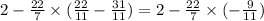
Следующим действием является умножение. Обе дроби являются отрицательными, значит их произведение будет положительным, так как при умножении минуса на минус бужет плюс. Сократим и умножим:
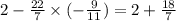
Осталось выполнить последнее действие, которым является сложение. Для начала приведём эти числа к общему знаменателю, сложим и выделим целую часть:
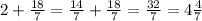
Вот и ответ.
3×х=(5/7)×11|×7
3×х×7=5×11
21×х=55|÷21
х=(55/21)
х=2(13/21)
2) 7÷r×6(1/5)=2
7÷r×(31/5)=2
(7×5)÷r×31=2
35÷r×31=2|×31×r
35=62×r|÷62
r=(35/62)
3) (5-x)*(x-4)=0
5x-20-x²+4x=0
-x²+9x-20=0|×(-1)
x²-9x+20=0
по теореме Виета:
х1+х2=-(-9)=9
х1×х2==20
х1=4
х2=5
через дескриминант:
D=(-(-9))²-4×1×20=81-80=1
x1=(-(-9)-√1)/2×1=(9-1)/2=8/2=4
x2=(-(-9)+√1)/2×1=(9+1)/2=10/2=5