Длина меньшего основания трапеции равна 3 см
Пошаговое объяснение:
(К сожалению, не удалось вставить чертёж, но он достаточно простой - чертим трапецию, нижнее основание AD, верхнее ВС, проводим в ней диагонали АС и BD, проводим среднюю линию MN. Точки Х и У - середины диагоналей лежат на средней линии MN. Вот и весь чертёж. Надеюсь, не составит труда его изобразить)
Дано:
ABCD – трапеция,
АС и AD – диагонали трапеции,
Х – середина АС, Y – середина BD.
ХY = 2 см, AD= 7см
Найти: ВС – меньшее основание трапеции
1. Докажем, что отрезок, соединяющий середины диагоналей трапеции равен полуразности оснований.
MX – средняя линия треугольника АВС, следовательно, MX=BC/2
NY – средняя линия треугольника DBC, следовательно, NY=BC/2
MN = (AD+BC)/2
XY=MN – MX – NY = (AD+BC)/2 – BC/2 – BC/2 = (AD-BC)/2
XY =(AD-BC)/2 (теперь это доказано)
2. Найдём ВС:
(AD-BC)/2=XY
AD-BC=2XY
В это выражение подставим значения AD=7 см и ХУ=2 см (из условия задачи):
7 –BC=2*2
7 – BC= 4
BC = 3 (см) - длина меньшего основания трапеции
5 часов
Пошаговое объяснение:
Первым действие рассчитает какую часть сосуда, кран A заполняет за 1 час.
Если принят сосуд за единицу, то за 1 час кран А заполнит 1/6 (1) сосуда.
Проделав тоже самое с кранами B и С, получим:
За 1 час кран В заполнит 1/8 (2) сосуда, а из крана С вытекает 1/12 (3) воды из сосуде.
В условии сказано, что "Первые два часа все три крана были открыты". То есть надо рассчитать какая часть сосуда будет заполнятся за час, если открыть три крана. Для этого мы суммируем значение (1) и (2) и отнимем от этого значение (3). Т.к вода из крана С(3) вытекает.
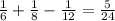
5/24 именно такая часть сосуда заполняется за 1 час, если открыть все 3 крана. За 2 часа соответственно в два раза больше:
5/24 * 2 = 5/12
Найдя количества воды, нам останется просто разделить на значение (3)
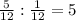
И мы получаем, что если первые два часа открыть все три крана, а затем закрыть краны А и В, то понадобиться еще 5 часов что бы вода полностью вытекла.