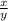Question

Кто впервые создал рациональные числа?

Answer 1

Трудно точно назвать фамилию человека, который первый создал рациональные числа, но можно примерно предположить историю их создания. ratio - в переводе  с латыни означает отношение, деление, дробь. значит рациональное число - это число представляемое дробью $\frac{x}{y}$, где x - целое число, а y - натуральное. это понятие возникло много тысяч лет назад, когда люди, измеряя длину, вес, площадь и т. д., пришли к выводу, что не всегда можно обойтись только целыми числами и необходимо ввести понятие доли: половина, четверть, треть. дробями и операциями над ними пользовались шумеры и египтяне, а от них этому научились греки.