2*12+3*10+3*7=24+30+21=75 детали выточил всего
2+3+3=8 чсаов работал всего
75/8=9 3/8 детали выточил за 1 час. (9 целых, три восьмых)
 .
.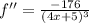 .
.
ответ: e².
Пошаговое объяснение:
1) Положим x-2=t⇒x=t+2 и при x⇒2 t⇒0. Тогда данное выражение примет вид: e²*(e^t-1)/t и требуется найти предел этого выражения при t⇒0. Так как предел e² равен e², то искомый предел равен e²*lim[(e^t-1)/t при t⇒0.
2) Положим e^t-1=z⇒t=ln(z+1) и при t⇒0 z⇒0. Тогда данный предел можно записать так: e²*lim[z/ln(z+1)]=e²/lim[ln(z+1)/z]. Обозначим A=lim[ln(z+1)/z] и рассмотрим B=e^A=lim{e^[ln(z+1)/z]}=lim[(z+1)^(1/z)]. Но предел в скобках [ ] есть ни что иное, как второй замечательный предел, равный e. Из равенства B=e^A=e находим A=1. Тогда искомый предел равен e²/A=e².
сколько деталей выточил за 2 часа
12*2=24 дет
сколько выточил за 3 часа
10*3=30 дет
сколько выточил за последние 3 часа
7*3=21 дет
сколько всего деталей
24+30+21= 75 деталей
сколько часов работал
2+3+3=8 час
сколько в среднем выточил за 1 час
75:8= 9,375 дет