Question

0в спортивную группу входят 9 лыжников, 8 конькобежцев,7 бегунов,11 прыгунов найти вероятность,что среди на удачу отобраны 6 спортсменов все лыжники 1 из коробки где 5 зеленых и 4 красных наудачу одновременно извлекают 3 шара найти вероятность что извлеченные шары будут одного цвета 2 из 2 коробок: в первой- 2 желтых и 4 черных во –второй 3 желтых и 5 черных. из первой коробки во вторую перекладывают,не глядя, один шар. после перемешивают из второй коробки вынимают один шар. найти вероятность,что этот шар черный

Answer 1

                                  Задача 0.

Всего в спортивной группе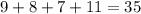 $9+8+7+11=35$ человек.  

Из них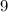 $9$ - лыжники.

P (первый выбранный - лыжник) = $9/35$.P (второй выбранный - лыжник) = $8/34$.P (третий выбранный - лыжник) = $7/33$...............................................................................P (шестой выбранный - лыжник) = $4/30$.

И все эти вероятности нужно перемножить, чтобы получить ту вероятность, которую нас просят в задаче:

P (все выбранные люди - лыжники) =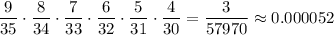 $\displaystyle \frac{9}{35} \cdot \frac{8}{34} \cdot \frac{7}{33} \cdot \frac{6}{32} \cdot \frac{5}{31} \cdot \frac{4}{30} = \frac{3}{57970} \approx 0.000052$.

                                 Задача 1.

P (все извлеченные шары одного цвета) = P (все извлеченные шары зеленые) + P (все извлеченные шары - красные).

P (все извлеченные шары - зеленые) =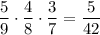 $\displaystyle \frac{5}{9} \cdot \frac{4}{8} \cdot \frac{3}{7} = \frac{5}{42}$.

P (все извлеченные шары - красные) =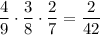 $\displaystyle \frac{4}{9} \cdot \frac{3}{8} \cdot \frac{2}{7} = \frac{2}{42}$.

P (искомая) =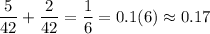 $\displaystyle \frac{5}{42} + \frac{2}{42} = \frac{1}{6} = 0.1(6) \approx 0.17$.

                                 Задача 2.

Искомую вероятность опять можно получить сложением двух других вероятностей:

P₁ = P (из первой коробки достали именно черный шар) · P (из второй коробки, в которой уже на 1 черный шар больше, тоже достали черный шар) =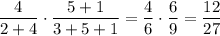 $\displaystyle \frac{4}{2+4} \cdot \frac{5+1}{3+5+1} = \frac{4}{6} \cdot \frac{6}{9} = \frac{12}{27}$.

P₂ = P (из первой коробки был извлечен желтый шар) · P (из второй, в которой теперь на 1 желтый шар больше, достали все же черный шар) =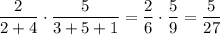 $\displaystyle \frac{2}{2+4} \cdot \frac{5}{3+5+1} = \frac{2}{6} \cdot \frac{5}{9} = \frac{5}{27}$.

P (искомая) =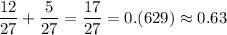 $\displaystyle \frac{12}{27} + \frac{5}{27} = \frac{17}{27} = 0.(629) \approx 0.63$.