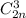
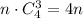 , так как призма имеет n боковых граней, и в каждой грани расположено 4 вершины. Число выбрать три вершины основания равно
, так как призма имеет n боковых граней, и в каждой грани расположено 4 вершины. Число выбрать три вершины основания равно 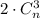 , так как призма имеет всего два основания и в каждом из этих оснований расположено n вершин.
, так как призма имеет всего два основания и в каждом из этих оснований расположено n вершин.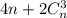 . Тогда число благоприятных исходов равно
. Тогда число благоприятных исходов равно 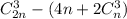 .
.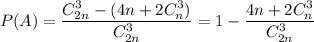
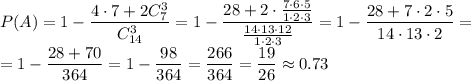
1 строчка.
Периметр (или же P) – сумма всех сторон.
7 + 7 + 20 + 20 = 54 км периметр.
Площадь (или же S) – это a умноженная на b.
7 × 20 = 140 км2. Площадь.
2 строчка.
Чтобы узнать длину, когда известен периметр и ширина, нужно ширину умножить на два, вычесть ее из периметра и результат разделить на два.
5 × 2 = 10 дм
32 - 10 = 22 дм
22 : 2 = 11 дм – длина.
Теперь по тому же принципу, что и в первом случае, находим площадь.
11 × 5 = 55 дм2 площадь.
3 строчка.
Чтобы узнать ширину прямоугольника, когда известна только площадь и длина, нужно S:a. (обратное тому, что a × b = S)
24 : 3 = 8 мм – ширина.
Периметр узнаем по тому же принципу, что и в первом случае.
3 + 3 + 8 + 8 = 22 мм – периметр.
Как нам известно, вероятность попадания равна 0.8
Значит, вероятность того, что будет выбран первый стрелок и оба выстрела окажутся успешными, равна 0.5*0.8*0.8 = 0.32
Вероятность того, что будет стрелять второй стрелок, равна 0.5
Как нам известно, вероятность попадания равна 0.7
Значит, вероятность того, что будет выбран первый стрелок и оба выстрела окажутся успешными, равна 0.5*0.7*0.7 =0.245
0.245 + 0.32 = 0.565