Пошаговое объяснение:1) f(x)= 2x²-3x+1 , [-1;1] ⇒ f'(x)= 4x-3, найдём критические точки: 4х-3=0, ⇒ х = 3/4=0,75 ∈[-1;1]. Найдём значения функции в критической точке и на концах данного промежутка: f(3/4)= 2·(3/4)²- 3·3/4 +1 =9/8 -9/4 + 1 = -1/8 ; f(1) = 0; f(-1)=6 ⇒ max f(x)=f(-1)=6; minf(x)=f(3/4)=-1/8
2)f(x)=3x²-4 на [2;4] ⇒ f'(x)=6x 6x=0, x=0-крит. точка, но x=0∉ [2;4] ⇒ Найдём значения функции на концах данного промежутка: f(2)= 3·2²-4= 12-4=8 f(4)=3·4² - 4= 48-4=44 ⇒ max f(x)=f(-4)=44; minf(x)=f(2)=8 3)f(x)=x²-1 на [0;3]⇒ f'(x)=2x , 2x=0 x=0 -критическая точка х=0 ∈ [0;3]. Найдём значения функции в критической точке и на концах данного промежутка: f(0) =0²-1=-1; f(3)=3²-1=8 ⇒max f(x)=f(3)=8; minf(x)=f(0)= -1
25
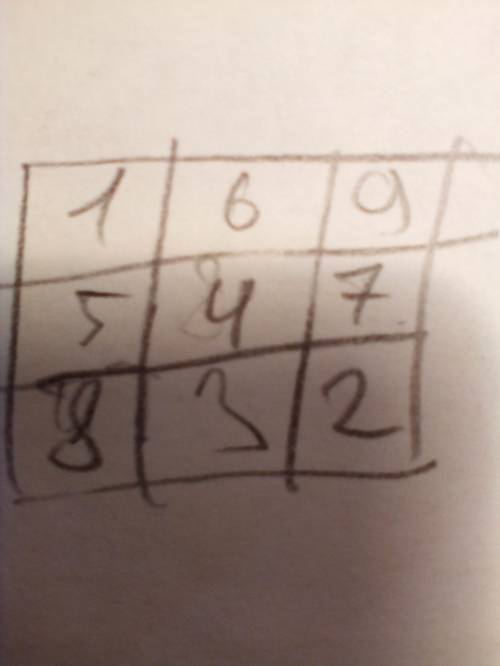
Пошаговое объяснение:
Чтобы получить в сумме 21 можно попробовать сложить 3 самых больших числа из данных: 7+8+9=24.
Не подошло. 24 больше 21 на 3, значит нужно одно из чисел уменьшить на 3. Если мы уменьшим 9, то получим 6.
6+7+8=21
Этот вариант не подойдёт, так как если мы впишем эти числа в диагональ в любой последовательности, то мы не сможем составить вторую диагональ, сумма чисел которой равна 7 (6+1=7, а нам нужно ещё 1 число).
Если мы уменьшим 8 из этого ряда на 3, то получим 5. Но и этот вариант не подойдёт всё по той же причине(5+2=7, а из двух или единиц не получится составить ряд, так у нас всего 9 не повторяющихся чисел)
Поэтому остаётся уменьшать только число 7:
7-3=4
Вот теперь мы сможем расположить ряд чисел так, чтобы получилось составить вторую диагональ.
4 поставим посередине, и тогда во второй диагонали получится 1, 4 и 2 (можно и 2, 4 и 1, главное, чтоб четвёрка было посередине)
Остальные числа вписываем в остальные клетки в любом порядке и складываем.
Обалдеть, я сама смогла это решить!
Сумма 5 клеток посередине будет 25, т. к. 3+4+5+6+7=25