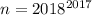 , а S(n) - это сумма цифр числа. Надо четыре раза подряд найти сумму цифр чисел, т.е. S(S(S(S(n)))).
, а S(n) - это сумма цифр числа. Надо четыре раза подряд найти сумму цифр чисел, т.е. S(S(S(S(n)))).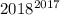 .
.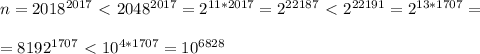
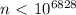
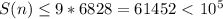
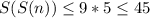
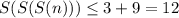
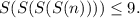
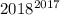 . четыре раза подряд просуммировать цифры, то результат не будет превышать 9!
. четыре раза подряд просуммировать цифры, то результат не будет превышать 9!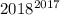 на 9, тем самым мы узнаем, какой остаток будет от деления суммы цифр
на 9, тем самым мы узнаем, какой остаток будет от деления суммы цифр 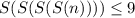 на 9. А это и будет ответ.
на 9. А это и будет ответ.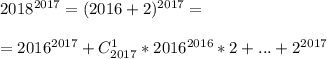
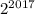 , делятся на 9 без остатка (туда входит число 2016).
, делятся на 9 без остатка (туда входит число 2016).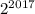 , чтобы появилась 9, затем разложим по формуле бинома Ньютона:
, чтобы появилась 9, затем разложим по формуле бинома Ньютона: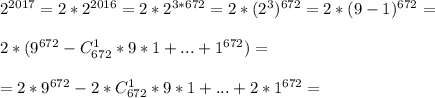
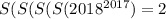
Выражением;
8•2+5•1+7•3+2•5= 16+5+21+10=52 Л заготовил варенья
По действиям
1)) 8•2=16л в 2л горшках
2)) 5•1=5л в 1л горшках
3)) 7•3=21л в 3л горшках
4)) 2•5=10л в 5л горшках
5)) 16+5+21+10=52л
ответ: великан заготовил 52л варенья
б)Каждый день в течение 5 дней великан съедал по 3 литра варенья и 4 дня по 6 литров.Сколько у него осталось варенья?
Выражением;
52-5•3-4•6=52-15-24= 52-39=13л осталось варенья
Или
52-(5•3+4•6)=52-39=13л
По действиям
1)) 5•3=15л съел за 5дней
2)) 4•6=24л съел за 4 дня
3)) 52-15-24=13л осталось
ответ: осталось 13л варенья
Если надо для а) и б) одно выражение
8•2+5•1+7•3+2•5 -5•3-4•6 =
16+5+21+10-15-24=13л осталось