) = -sin(
) = -cos(x).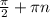 
, n ∈ Z.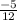 
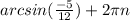, n ∈ Z. 
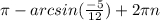, n ∈ Z. , 
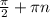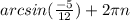, π 
, n ∈ Z.
Вычислим координаты векторов:
AB = { 3 - 1 ; -1 - (-1) ; 1 - 3 } = { 2 ; 0 ; -2 } ,
BC = { -1 - 3 ; 1 - (-1) ; 3 - 1 } = { -4 ; 2 ; 2 } .
Найдем скалярное произведение векторов:
AB · BC = ABx · BCx + ABy · BCy + ABz · BCz = 2 · (-4) + 0 · 2 + (-2) · 2 = (-8) + 0 + (-4) = -12 .
Вычислим длины обоих векторов:
|AB| = √(AB²x+ AB²y+ AB²z) = √(2² + 0² + (-2)²)= √(4 + 0 +4 ) = √8 = 2,8284 ,
|BC| = √(BC²x+ BC²y+ BC²z) = √((-4)² + 2² + 2²) = √(16 + 4 + 4) = √24 = 4,899 .
Подставим длины векторов и их скалярное произведение в формулу:
cos(α)=(AB · BC)/(|AB| · |BC|) = -12 /(√8 · √24 ) = -0,866.
cos(α) = -0,866 .
α ≈ 2,618 рад. = 150°.
х45%
х=380*45/100=171
2)(299,3:14,6-9,62)*3,5+72,2=(20,5-9,62)*3,5+72,2=10,88*3,5+72,2=38,08+72,2=110,28
3)х100%
117018%
х=1170*100/18=6500
4)6,7у+13+3,1у=86,5
3,1у+6,7у=86,5-13
9,8у=73,5
у=7,5