допустим получены данные числа с разностью z:
a1=x-z= 8-5=3
a2=x=8
a3=x+z=8+5=13
(откуда были получены эти цифры, смотрите ниже. подставляем эти цифры в формулу для вычисления суммы десяти членов прогрессии.)
до преобразований:
x-z+2
x+2
x+z+7
x-z+2+x+2+x+z+7=35
3x=24
x=8
подставляем в вышенаписанные выражения:
10-z
10
15+z
по свойству геометрической прогрессии:
10²=(10-z)(15+z)
z²+5z-50=0
по теореме Виета имеем два корня, один из которых отрицательный (-10), не подходит, т.к в условии задачи написано, что прогрессия возрастающая (а при -10 прогрессия будет убывающей), второй корень 5.
z1=-10
z2=5
выбираем, естественно, положительный корень уравнения.
S10= (2a1+9d / 2)*10= (2*3+9*5 / 2)*10=(6+45)*5=51*5=255
ОТВЕТ: 255, вариант С.
ДАНО
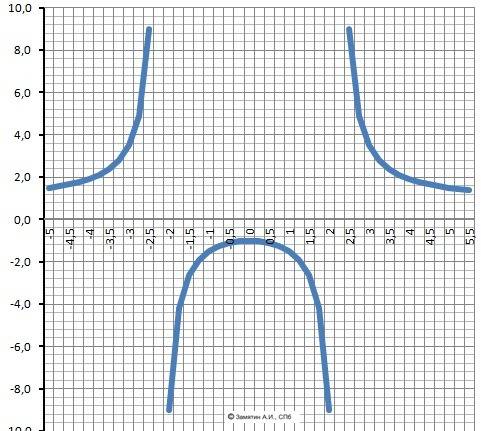
Y= (x²+5)/(x²-5)
1.Область определения - Х∈(-∞;- √5)∪(-√5;√5)∪(√5;+∞)
2. Пересечение с осью Х - нет.
3. Пересечение с осью У. У(0) = -1.
4. Поведение на бесконечности.limY(-∞) = 1 limY(+∞) = 1,
limY(-√5-) = +∞, limY(-√5+) = -∞, limY(√5-) = -∞, limY(√5+) = +∞,
5. Исследование на чётность.Y(-x) = Y(x).
Функция чётная.
6. Производная функции.
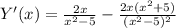
7. Корень при Х=0. Максиммум – Ymax(0)=-1.
Возрастает - Х∈(-∞;-√5)∪(-√5;0) , убывает = Х∈(0;√5)∪(√5;+∞).
8. Вторая производная - Y"(x) = ?
9. Точек перегиба - нет.
Выпуклая “горка» Х∈(-√5;√5),Вогнутая – «ложка» Х∈(-∞;-√5))∪(√5;+∞).
10. График в приложении.
1,5х для 6
х+1,5х=715
2,5х=715
х=286уч. для 5 класса
286*1,5=429уч. для 6 класса