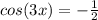
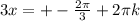
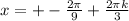
Одним из наиболее мощных методов интегрирования является замена переменной в интеграле. Поясним суть этого метода. Пусть F'(x)=f(x), тогда
\int f(x)\,dx= \int F'(x)\,dx= \int d\bigl(F(x)\bigr)=F(x)+C.
Но в силу инвариантности формы дифференциала равенство d\bigl(F(x)\bigr)=F'(x)\,dx= f(x)\,dx остается справедливым и в случае, когда {x} — промежуточный аргумент, т.е. x=\varphi(t). Это значит, что формула \textstyle{\int f(x)\,dx=F(x)+C} верна и при x=\varphi(t). Таким образом,
\int f\bigl(\varphi(t)\bigr)\,d\bigl(\varphi(t)\bigr)= F\bigl(\varphi(t)\bigr)+C, или \int f\bigl(\varphi(t)\bigr)\varphi'(t)\,dt= F\bigl(\varphi(t)\bigr)+C.
Итак, если F(t) является первообразной для f(x) на промежутке {X}, а x=\varphi(t) — дифференцируемая на промежутке {T} функция, значения которой принадлежат {X}, то F\bigl(\varphi(t)\bigr) — первообразная для f\bigl(\varphi(t)\bigr)\varphi'(t),~t\in T, и, следовательно,
\int f\bigl(\varphi(t)\bigr)\varphi'(t)\,dt= \int f(x)\,dx\,.
Эта формула позволяет свести вычисление интеграла \textstyle{\int f\bigl(\varphi(t)\bigr)\varphi'(t)\,dt} к вычислению интеграла \textstyle{\int f(x)\,dx}. При этом мы подставляем вместо \varphi(t) переменную {x}, а вместо \varphi'(t)\,dt дифференциал этой переменной, т. е. dx. Поэтому полученная формула называется формулой замены переменной под знаком неопределенного интеграла. Она используется на практике как "слева направо", так и "справа налево". Метод замены переменной позволяет сводить многие интегралы к табличным. После вычисления интеграла \textstyle{\int f(x)\,dx} надо снова заменить {x} на \varphi(t).
Пример 1. Вычислим \int\cos2t\,dt.
Решение. Введем новую переменную {x}, положив 2t=x. Тогда 2\,dt=dx,~dt=\frac{1}{2}\,dx и, следовательно,
\int\cos2t\,dt= \int\cos{x}\,\frac{1}{2}\,dx= \frac{1}{2}\int\cos{x}\,dx= \frac{1}{2}\sin{x}+C= \frac{1}{2}\sin2t+C.
Замечание. Вычисление короче записывают так:
\int\cos2t\,dt= \frac{1}{2}\int\cos2t\,d(2t)= \frac{1}{2}\sin2t+C.
Пошаговое объяснение:
1наб.(1Х + 2М + 3Ч) ? руб; но<2 наб. на 64000 руб
2наб.(3Х +2М + 1Ч) ? руб
Х - Ч = ? руб
Решение.
Приравняем второй набор к первому, учитывая разницу:
3Х + 2М + 1Ч = Х + 2М + 3Ч + 64 000 руб.
Так как микроволновые печи входят в оба набора и вносят одинаковые суммы денег в наборы, их можно исключить из равенства:
ЗХ + 1Ч = Х + 3Ч + 64 000 (руб)
Мы можем также исключить из обеих частей равенства по холодильнику и по чайнику, это не повлияет на равенство:
2Х = 2Ч + 64 000 (руб);
Если в правой и левой частях все уменьшим в 2 раза, равенство так же сохранится:
Х = Ч + 32 000 (руб),
А это означает, что холодильник дороже чайника на 32 тысячи рублей:
Х - Ч = 32 000 руб.
ответ: на 32 тысячи рублей холодильник дороже чайника.