К сожалению, не могу Вам нарисовать. Не поддерживает мой браузер таких операций. Но все же. постараюсь объяснить.
Пусть точки К и Т- основания перпендикуляров ОК и ОТ, проведенных к сторонам АВ и АС соответственно. ОК=ОТ- по условию, а АО- общая, тогда треугольники АОК и АОТ равны по катету и гипотенузе, а в равных треугольниках против равных сторон лежат равные углы, т.к. КО=ТО, то Угол КАО=углу ТАО, но это доказывает, что АО - биссектриса угла КАТ, а, значит, и угла АВС, а точка О- лежащая на этой биссектрисе точка.
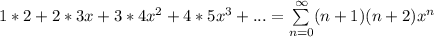
Это степенной ряд, найдём его радиус сходимости.
Согласно признаку Даламбера.
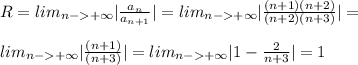
Так как радиус сходимости степенного ряда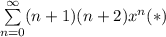 
равен 1, то при |x| >1, ряд расходится.
Проверим сходимость в точках x = 1 и x = -1.
При x = 1, ряд (*) — расходится (так как не выполняется необходимое условие сходимости числового ряда).
При x = -1, ряд (*) – расходится (так как не выполняется необходимое условие сходимости числового ряда).
Ряд сходится при |x| < 1.
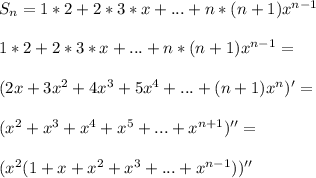
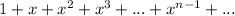- разложение в ряд Маклорена функции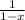 
См. дальнейшее решение во вложении.
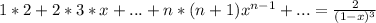при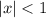 
s=(120+x)*5/6
Откуда:x=6s/5 -120
Теперь составим уравнение:
s/120 +1,25=s/(6s/5-120)
(150+s)/120=s/((6s-600)/5)=5s/(6s-600)
(150+s)(6s-600)=600s
(150+s)(s-100)=100s
150s-15000+s^2-100s-100s=0
s^2-50s-15000=0
D=2500+60000=62500=250^2
s=(50+-250)/2
s=150 км
s=-100 не подходит
ответ:150 км