Пошаговое объяснение:
1) определим уравнение касательной проведенной к графику данной функции в точке с абциссой x₀=2 по формуле y=y₀+y'(x₀)(x-x₀)
y₀=y(2)=2*2-2²=4-4=0 ; y'=2-2x ; y'(2)=2-4=-2
y=-2(x-2)=-2x+4 ; y=-2x+4
2) найдем точки пересечения графиков y=-2x+4 и y=2x-x²
-2x+4=2x-x²
x²-2x+4-2x=0
x²-4x+4=0
(x-2)²=0
x=2
(2;0)
3) найдем точки пересечения графика y=2x-x² с ОХ
y=2x-x²=0
х(2-х)=0
x₁=0 ; x₂=2
4) найдем точкy пересечения графика y=-2x+4 с ОУ
х=0 ; y=-2x+4=-2*0+4=4
(0;4)
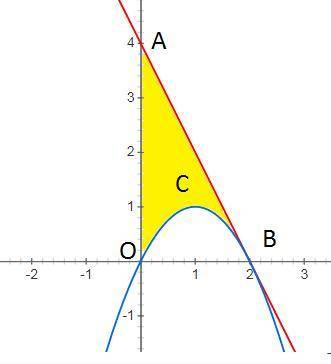
5) схематически построим графики y=-2x+4 и y=2x-x²
6) площадь фигуры ограниченной линиями y=2x-x^2 и касательной проведенной к графику данной функции в точке с абциссой x=2 и с осью ординат
S=SΔOAB-SкриволинейногоΔOCB=
2 2 2
= (OA*OB/2)-∫(2x-x²)dx=(4*2/2)-[(2x²/2)-(x³/3)]=4-[x²-(x³/3)]=
0 0 0
=4-[2²-(2³/3)]=4-[4-(8/3)]=4-4+8/3=8/3=2 2/3
Рассмотрим сложенный из дощечкек квадрат на листочке в клеточку и увидим, что:
а - большая сторона параллелограмма,
а - основание маленького треугольника,
а - боковое ребро среднего треугольника
2а - основание большого треугольника,
b - меньшая сторона параллелограмма,
b - сторона маленького квадрата,
b - сторона маленького треугольника,
2b - основание среднего треугольника
2b - боковое ребро большого треугольника.
Посчитаем периметры отдельных фигур:
1) периметр большого треугольника:
2а + 2b + 2b = 2a + 4b
2) периметр среднего треугольника:
а + а + 2b = 2a + 2b
3) периметр маленького треугольника:
b + b + a = 2b + a
4) периметр маленького квадрата:
4b
5) периметр параллелограмма:
2а + 2b.
Теперь рассмотрим сложную фигуру.
Итак:
1) слева внизу большой треугольник, из периметра которого надо исключить меньшую сторону параллелограмма:
2а + 4b - b = 2a + 3b
2) на основании большого треугольника расположены параллелограмм, из которого имеют значение только две стороны а и b, и маленький треугольник, из которого имеет значение только боковая сторона b
a + b + b = a + 2b
3) из маленького квадрата в центре фигуры имеет значение только две стороны b:
Но поскольку заданная сложная фигура симметрична, несмотря на то, что ее левая и правая стороны сложены из разных фигур, мы можем учесть только одну сторону маленького квадрата b, найти периметр половины сложной фигуры и умножить на 2.
Найдем периметр сложной фигуры:
1) 2а + 3b + a + 2b + b = 3a + 6b = 3(a + 2b) - полупериметр сложной фигуры.
2) 2 • 3(a + 2b) = 6(a + 2b) или 6а + 12b
ответ: 6(a + 2b) или 6а + 12b.
х - было денег у каждого сначала
у - осталось у Васи, тогда
3у - осталось у Маши
Составим систему:
из первого уравнения:
у = х - 14
подставим во второе:
х - 6 = 3(х - 14)
х - 6 = 3х - 42
42 - 6 = 2х
2х = 36
х = 18 рублей было у каждого сначала
______________
проверим:
18 - 14 = 4 руб. - осталось у Васи
18 - 6 = 12 руб. - осталось у Маши
12 : 4 = 3 - в три раза больше осталось у Маши.
_______________________________________________
решение второй задачи:
во втором ящике Х
в первом ящике 7х
остаток в первом ящике У
система:
7х - 38 = у
х - 14 = у - 78
из первого уравнения:
у = 7х - 38
подставляем во второе:
х - 14 = 7х - 38 - 78
х - 7х = 14 - 38 - 78
6х = 102
х = 17 - во втором ящике
17 * 7 = 119 - в первом ящике
_______________
проверка:
119 - 38 = 81
17 - 14 = 3
81 - 3 = 78