При каких значениях х, производная функции f(x)=корень третей степени из x^2 равна 1

👇

Увидеть ответ

Ответ:

Bekarys2002

04.02.2022

Производная:
(x^2/3)'=2/3 *x^2/3 -1=2/3 *x^-1/3
2/3 *x^-1/3=1
x^-1/3=3/2
x^1/3=2/3
x=8/27

4,5(4 оценок)

Открыть все ответы

Ответ:

Элизабет3000000

04.02.2022

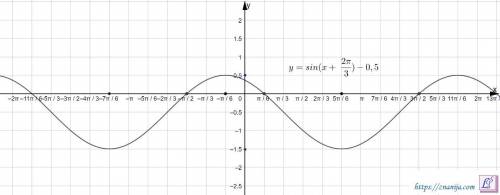
График функции 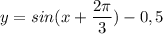$\displaystyle y = sin(x+\frac{2\pi }{3}) -0,5$ получается сдвигом графика 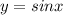$\displaystyle y = sinx$ вдоль оси OX на 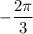$\displaystyle-\frac{2\pi }{3}$ единиц и вдоль оси OY на -0,5 единиц.

Свойства функции 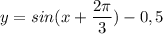$\displaystyle y = sin(x+\frac{2\pi }{3}) -0,5$ .

1) Область определения функции x ∈ (-∞; +∞).

2) Область значений функции y ∈ [-1,5; 0,5].

3) Периодичность. Функция периодическая с периодом T = 2π.

4) Четность функции не определенная (не является четной, не является нечетной).

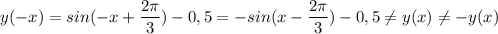
$\displaystyle y(-x) = sin(-x+\frac{2\pi }{3}) -0,5= -sin(x-\frac{2\pi }{3}) -0,5\neq y(x)\neq -y(x)$

5) Нули функции.

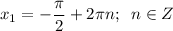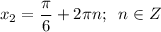
y = 0 при $\displaystyle x_{1} = -\frac{\pi }{2}+2\pi n ; \;\;n \in Z$ и $\displaystyle x_{2} = \frac{\pi }{6}+2\pi n ; \;\;n \in Z$

Решение

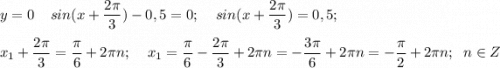
$\displaystyle y=0 \;\;\;\;sin(x+\frac{2\pi }{3}) -0,5=0; \;\;\;\;sin(x+\frac{2\pi }{3}) =0,5; \\\\x_{1} +\frac{2\pi }{3}=\frac{\pi }{6} +2\pi n ;\;\;\;\;x_{1} =\frac{\pi }{6} -\frac{2\pi }{3}+2\pi n =-\frac{3\pi }{6}+2\pi n= -\frac{\pi }{2}+2\pi n ; \;\;n \in Z$

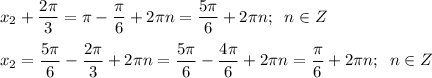
$\displaystyle x_{2} +\frac{2\pi }{3}=\pi -\frac{\pi }{6} +2\pi n=\frac{5\pi }{6}+2\pi n ; \;\; n \in Z\\\\x_{2} =\frac{5\pi }{6} -\frac{2\pi }{3}+2\pi n =\frac{5\pi }{6}-\frac{4\pi }{6} +2\pi n= \frac{\pi }{6}+2\pi n ; \;\;n \in Z$

6) а) Наибольшее значение функции y = 0,5 при 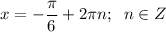$\displaystyle x = -\frac{\pi }{6}+2\pi n ; \;\;n \in Z$

б) Наименьшее значение функции y = -1,5 при 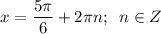$\displaystyle x = \frac{5\pi }{6}+2\pi n ; \;\;n \in Z$

7) а) Функция убывает при $\displaystyle x \in[ -\frac{\pi }{6}+2\pi n ; \;\;\frac{5\pi }{6}+2\pi n] \;\;n \in Z$

б) Функция возрастает при $\displaystyle x \in[ -\frac{7\pi }{6}+2\pi n ; \;\;-\frac{\pi }{6}+2\pi n] \;\;n \in Z$

8) Промежутки знакопостоянства

y > 0 при 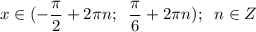$\displaystyle x \in( -\frac{\pi }{2}+2\pi n ; \;\;\frac{\pi }{6}+2\pi n); \;\;n \in Z$

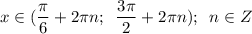
y < 0 при $\displaystyle x \in( \frac{\pi }{6}+2\pi n ; \;\;\frac{3\pi }{2}+2\pi n) ;\;\;n \in Z$

Математика 10 класс по максималки при решении всего! (И 1, и 2-го и всего)Сама функция: y=sin(x+)-0,

4,6(26 оценок)

Ответ:

1231231221312223

04.02.2022

Пусть Петя задумал самое большое из данных натуральных чисел – 99 (нечетное). Как его определить, задав Пете не более 7 вопросов? 1) Является ли число четным? ответ: нет Осталось рассмотреть 50 нечетных чисел. 2) Получится ли остаток 1 при делении числа на 4? ответ: нет. Осталось рассмотреть 25 чисел при делении на 4 дающих остаток 3: 3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59, 63, 67, 71, 75, 79, 83, 87, 91, 95, 99. 3) Получится ли остаток 3 при делении числа на 8? ответ: да. Следовательно, поиск ведем среди 13 чисел: 3, 11, 19, 27, 35, 43, 51, 59, 67, 75, 83, 91, 99. 4) Получится ли остаток 3 при делении на 16? ответ: да. Значит, искомое число находится среди 7 чисел: 3, 19, 35, 51, 67, 83, 99. 5) Получится ли остаток 3 при делении числа на 32? ответ: да. Остается 4 числа: 3, 35, 67, 99. 6) Получится ли остаток 3 при делении числа на 64? ответ: нет. Остается 2 числа: 35 и 99. 7) Является ли число 35 ответом? ответ: нет. В таком случае искомым является число 99. Аналогичные рассуждения будут и в случае других задуманных нечетных чисел, и в случае ответа «да» на первый вопрос, т. е. когда задумано какое-либо четное число.

4,7(63 оценок)

Это интересно:

Кулинария-и-гостеприимство

27.04.2022

Лимонно-медовая вода: не только вкусно, но и полезно...

Кулинария-и-гостеприимство

22.07.2021

Как сделать печенье «Отпечаток»...

Компьютеры-и-электроника

17.08.2022

Как сделать сайт в Word: подробное руководство...

Здоровье