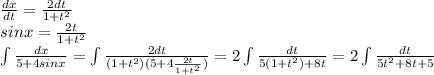
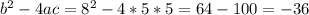
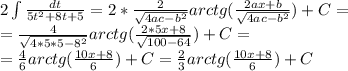

РЕШЕНИЕ: Пусть длина расстояния L.
Если Ваня стоит неподвижно на ступени эскалатора, то скорость движения равна L/60. (Считаем в секундах, в минуте 60 секунд).
Если Ваня взбегает по ступеням неподвижного эскалатора, то скорость движения равна L/40.
Когда Ваня бежит по ступеням движущегося эскалатора, то скорости Вани и эскалатора суммируются: L/60+L/40. Тогда время определяется отношением длины к скорости:
ОТВЕТ: 24 секунды вроде так
Задание № 5:
Стоя неподвижно на ступени эскалатора в метро Ваня поднимается наверх за одну минуту. Взбегая по ступеням неподвижного эскалатора, он добирается до верха за 40 секунд. За какое время Ваня поднимается наверх, если начинает взбегать по ступеням эскалатора, движущегося вниз? Дайте ответ в секундах.
РЕШЕНИЕ: Пусть длина расстояния L.
Если Ваня взбегает по ступеням неподвижного эскалатора, то скорость движения равна L/40. (Считаем в секундах, в минуте 60 секунд).
Если Ваня стоит неподвижно на ступени эскалатора, то скорость движения равна L/60.
Когда Ваня бежит по ступеням движущегося вниз эскалатора, то скорости Вани и эскалатора вычитаются: L/40-L/60. Тогда время определяется отношением длины к скорости:
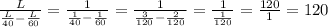
ОТВЕТ: 120 секунд