![y=(x^2-5x+5)e^7-x \\ \\ y'=(x^2-5x+5)'*e^7-(x)'=[(x^2)'-(5x)'+(5)']*e^7-1= \\ =(2x-5)*e^7-1 \\ \\ (2x-5)*e^7-1=0 \\ (2x-5)*e^7=1 \\ 2x-5=\frac{1}{e^7} \\ 2x=\frac{1}{e^7}+5 \\ x=\frac{1+5e^7}{2e^7} \\ x=2,5](/tpl/images/0280/5716/454fe.png)
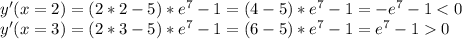
В четырехугольнике ABCD сторона AВ = у см
1) Составим выражения для сторон четырехугольника:
а) ВС на 2 см меньше АВ, то есть ВС = АВ - 2 см = у см - 2 см = (у - 2) см;
б) СD в 1,25 раза больше АВ, то есть СD = 1,25 · АВ = 1,25 · у см;
с) АD на 3 см больше СD, то есть АD = СD + 3 см = 1,25 · у см + 3 см =(1,25 · у + 3) см.
2) Периметр четырехугольнике ABCD равен 23,5 см, то есть:
Р=AB+BC+CD+AD=23,5 см
Подставляя выражения сторон из пункта 1) получаем уравнение:
у + (у - 2) + 1,25 · у + (1,25 · у + 3) = 23,5
3) Упростим и решаем уравнение
у + (у - 2) + 1,25 · у + (1,25 · у + 3) = 23,5
у + у - 2 + 1,25 · у + 1,25 · у + 3 = 23,5
4,5 · у + 1 = 23,5
4,5 · у = 23,5 - 1
4,5 · у = 22,5
у = 22,5 : 4,5
АВ = у = 5 см.
у`=(2x-5)e^(7 –x)+(x^2-5x + 5)e^(7 –x)*(-1)=(2x-5-x^2+5x - 5)e^(7 –x)=(-x^2+7x - 10)e^(7 –x)
y`=0 при х1=2 и при х2=5
у''=(-2x+7)e^(7 –x)+(-x^2+7x - 10)e^(7 –x)*(-1) = (-2x+7+x^2-7x + 10)*e^(7 –x)= (-9x+17+x^2)*e^(7 –x)
у''(х=2)=(-9*2+17+2^2)*e^(7 –2)=3*e^(5) > 0 - точка минимума
у''(х=5)=(-9*5+17+5^2)*e^(7 –5)=-3*e^(5) < 0 - точка максимума
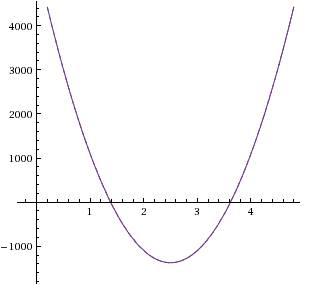
ответ при х=2 - точка минимума
во вложении - график