Пошаговое объяснение:
1) Докажем существование прямой.
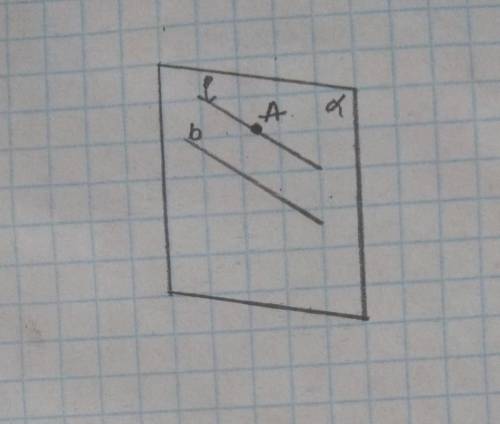
Пусть дана прямая b и точка А, не лежащая на этой прямой. Тогда через них проходит единственная плоскость a(см. рисунок). В этой плоскости, как известно из планиметрии, существует прямая l, проходящая через точку А и параллельная прямой b.
2. Докажем единственность прямой.
Предположим, что существует ещё одна прямая l1, проходящая через точку А и параллельная прямой b. Тогда прямая l1 должна лежать в одной плоскости с точкой А и прямой b, тоесть в плоскости а. Из курса планиметрии известно, что в плоскости а через точку А проходит единственная прямая, параллельная прямой b. Значит, прямая l1 совпадает с прямой l.
Теорема доказана