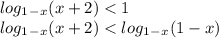
ОДЗ:
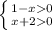 1-x ≠ 1
1-x ≠ 1
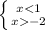 x ≠ 0
x ≠ 0
x ∈ (-2;0) ∪ (0 ; 1)
Теперь рассмотрим два случая:
1)
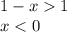
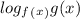 при
при 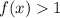 монотонно возрастает, соответственно мы имеем право опустить логарифмы без изменения знака неравенства
монотонно возрастает, соответственно мы имеем право опустить логарифмы без изменения знака неравенства
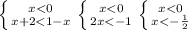
x ∈ ( -∞ ; -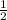 )
)
2)
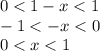
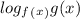 при
при 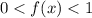 монотонно убывает, соответственно мы имеем право опустить логарифмы, изменив знак неравенства.
монотонно убывает, соответственно мы имеем право опустить логарифмы, изменив знак неравенства.
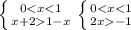
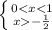
x ∈ (0 ; 1)
Теперь осталось пересечь наши решения с ОДЗ:
x ∈ ( -2 ; 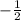 ) ∪ ( 0 ; 1 )
) ∪ ( 0 ; 1 )
ответ: x ∈ ( -2 ; 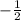 ) ∪ ( 0 ; 1 )
) ∪ ( 0 ; 1 )
UPD: знаю, что можно было решить намного проще с метода рационализации, но почему-то не все учителя принимают его, поэтому я расписал классическим
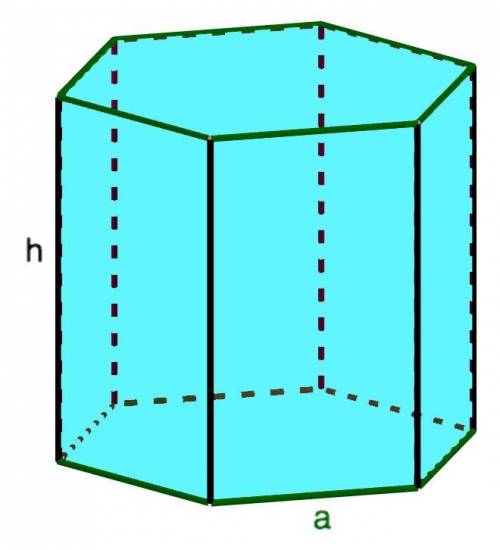
Объем полной поверхности правильной шестиугольной призмы равен 415,7 см3, а площадь 323,1 см2.
Пошаговое объяснение:
У правильной шестиугольной призмы основанием является правильный шестиугольник, где боковые грани перпендикулярны основаниям.
Объем правильной шестиугольной призмы равен произведению площади правильного шестиугольника, лежащего в основании, на высоту призмы, где высота призмы - это её боковое ребро.
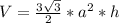
У нас боковое ребро 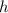 равно 10 см, а ребро основания
равно 10 см, а ребро основания  равно 4 см (как наглядно показано на рисунке). Подставляем и считаем:
равно 4 см (как наглядно показано на рисунке). Подставляем и считаем:
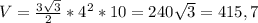 см3.
см3.
Правильная шестиугольная призма имеет два основания, где ее основания - правильные шестиугольники со стороной  , и шесть боковых сторон, которые представляют из себя прямоугольники со сторонами
, и шесть боковых сторон, которые представляют из себя прямоугольники со сторонами  и
и 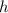 .
.
Поэтому площадь полной поверхности правильной шестиугольной призмы равна сумме площадей ее двух оснований и шести площадей боковых граней призмы.
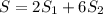
Где площадь основания находится согласно формуле:
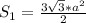
А площадь боковых граней равна: 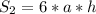
Подставляя это в формулу общей площади получим:
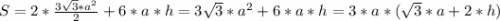
Подставляя наши значения получаем:
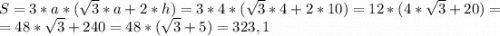 см2.
см2.
Получаем ответ: объем полной поверхности правильной шестиугольной призмы равен 415,7 см3, а площадь 323,1 см2.