Дан куб ABCDA1B1C1D1 и точки M,N,P- середины ребер А1В1, В1С1, DC. Найти угол между прямыми MN и A1P.
Поместим куб в систему координат вершиной В в начало, стороной ВА по оси Ох, стороной ВС по оси Оу. Размер ребра примем 2.
Определяем координаты точек.
M( 1; 0; 0), N(0;1;2). Вектор MN = (-1; 1; 2).
A1(2;0; 2), P(1; 2; 0). Вектор A1P = (-1; 2; -2).
Угол MN _ A1P
Модуль скалярного произведения а*в = |(1 + 2 - 4)| = |-1| = 1.
Модуль а. в = √(1+1+4)*√(1+4+4) = √6*3 = 7,34847.
cos a_b = 1/(3√6) = 0,1361.
a_b радиан = 1,4343.
a_b градус = 82,1788.
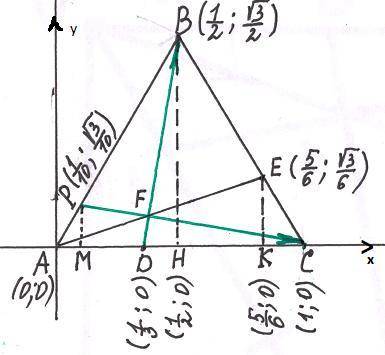
В равностороннем треугольнике ABC на сторонах AC и BC отметили точки D и E такие, что CD=2AD, BE=2CE. Обозначим точку пересечения отрезков AE и BD через F. Чему равен угол BFC?
Пошаговое объяснение:
1) Введем прямоугольную систему координат .Пусть АВ=ВС=АС=1. Пусть FC∩АВ=Р .Пусть ЕК⊥АС, ВН⊥АС, РМ⊥АС.
2) Определим координаты точек .
А(0;0) ,В(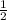
;
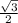) ,С(1;0) ,Н(0,5 ;0) ,D( 
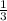;0) ,К( 
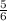;0) , Е(
3)Найдем координаты направляющих векторов: DB(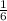 
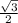; ) , РС( 
;
).
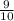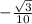4)Найдем скалярное произведение векторов .
DB *РС= * + *( ) =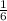
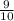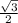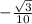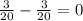⇒вектор DB⊥PC ⇒∠BFC=90°.
=======================================
Пояснения( жуткие вычисления , слабонервным можно не читать).
1) Координаты точки Е. ΔКСЕ прямоугольный .
КЕ=СЕ*sin60= *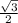 
.
КС=СЕ*cos60=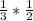 
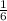= , поэтому АК= 1-
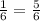→ Е( ;
) .
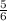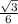2)Координаты точки В. ΔАВН- прямоугольный .
АН=НС= .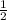
ВН=АВ*sin60=1* =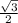
3)Ищем координаты точки Р
а)ΔВDC , по т. Менелая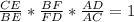 
, 
, 
.
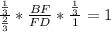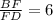б)ΔАВD , по т. Менелая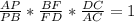 
, 
, 
,
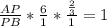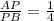AP=
= 
.
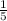в)ΔАРМ прямоугольный .
РМ=АР*sin60= * =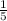 
.
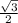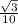АМ=АР*cos60=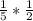 
=
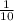→ P ( ; ) .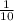
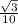18x:6=7
18x=6*7
18x=42
x=42:18
x=2,(3)
ответ:x=2,(3)