Канонические уравнения прямой имеют вид:
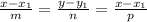
где m, n, р - координаты направляющего вектора прямой, x1, y1, z1 - координаты какой-либо точки, принадлежащей прямой.
Прямая задана как линия пересечения двух плоскостей. Чтобы найти точку, принадлежащую прямой, фиксируем одну из координат (проще всего положить, например, x=0) и полученную систему решаем как систему линейных уравнений с двумя неизвестными.
Итак, пусть x=0, тогда:
{-2y + 3z +15 = 0, |x3 = -6y + 9z + 45 = 0.
{3y - 4z - 12 = 0 . |*2 = 6y - 8z - 24 = 0.
1z + 21 = 0
z = -21, y = (3z + 15)/2 = (3*(-21) + 15)/2 = -48/2 = -24.
Найдены координаты точки М(x1, y1, z1 ), принадлежащей данной прямой: M (0, -24, -21).
Направляющий вектор прямой легко найти, зная нормальные векторы исходных плоскостей n1(1, -2, 3) и n2(2, 3, -4).
Так как прямая принадлежит одновременно обеим плоскостям, то ее направляющий вектор ортогонален нормальным векторам обеих плоскостей, то есть, он находится как их векторное произведение.
I j k| i j
1 -2 3| 1 -2
2 3 -4| 2 3 = 8i + 6j + 3k + 4j - 9i + 4k =
= -1i + 10j + 7k = (-1; 10; 7).
Канонические уравнения прямой имеют вид:
x/(-1) = (y + 24)/10 = (z + 21)/7.
Всего белых шаров: 10-3 = 7
Общее число возможных элементарных исходов для данных испытаний равно числу которыми можно извлечь 2 шаров из 10:
10!/2!8!=45
1. Найдем вероятность того, что среди выбранных 2 шаров один белый.
Подсчитаем число исходов, благоприятствующих данному событию:
а) один шар среди 7 белых можно выбрать количество которых равно:
7!/1!6!= 7
б) Остальные 1 черные шары можно выбрать из 3 черных:
3!/1!2!=3
1. Найдем вероятность того, что среди выбранных 2 шаров 1 белых.
Количество вариантов выбора из 7 белых шаров:
7!/1!6!= 7
Количество вариантов выбора из 3 черных шаров остальные 1 черных:
3!/1!2!=3
ответ:7*3/45=0,467
2) 1150·(2/5)=460 петушков
3) 1150-460=690 курочек