ответ:
алгоритм исследования функции двух переменных на экстремум
функция z = f(x,y) имеет максимум в точке m0(x0; y0), если f(x0; y0) > f(x; y) для всех точек (x; y), достаточно близких к точке (x0; y0) и отличных от неё. функция z = f(x,y) имеет минимум в точке m0(x0; y0), если f(x0; y0) < f(x; y) для всех точек (x; y), достаточно близких к точке (x0; y0) и отличных от неё. максимум и минимум функции называются экстремумами функции.
исследование функции двух переменных на экстремум проводят по следующей схеме.
1. находят частные производные dz/dx и dz/dy.
2. решают систему уравнений:
и таким образом находят критические точки функции.
3. находят частные производные второго порядка:
4. вычисляют значения этих частных производных второго порядка в каждой из найденных в п.2 критических точках m(x0; y0).
5. делаю вывод о наличии экстремумов:
а) если ac – b2 > 0 и a < 0 , то в точке m имеется максимум;
б) если ac – b2 > 0 и a > 0 , то в точке m имеется минимум;
в) если ac – b2 < 0, то экстремума нет;
г) если ac – b2 = 0, то вопрос о наличии экстремума остается открытым;
пример №1. найти экстремумы функции f(x,y)=x3+xy2+x2+y2 и определить по критерию сильвестра их тип.
решение.
1. найдем первые частные производные.
2. решим систему уравнений.
3x2+2x+y2=0
2xy+2y=0
получим:
а) из первого уравнения выражаем x и подставляем во второе уравнение:
x = -1
y2+1=0
данная система уравнений не имеет решения.
б) из первого уравнения выражаем y и подставляем во второе уравнение:
или
или
откуда x1 = -2/3; x2 = 0; x3 = -2/3; x4 = 0
данные значения x подставляем в выражение для y. получаем: y1 = 0; y2 = 0; y3 = 0; y4 = 0
количество критических точек равно 2: m1(-2/3; 0), m2(0; 0)
3. найдем частные производные второго порядка.
4. вычислим значение этих частных производных второго порядка в критических точках m(x0; y0).
вычисляем значения для точки m1(-2/3; 0)
ac - b2 = -4/3 < 0, то экстремума нет.
вычисляем значения для точки m2(0; 0)
ac - b2 = 4 > 0 и a > 0 , то в точке m2(0; 0) имеется минимум z(0; 0) = 0
вывод: в точке m2(0; 0) имеется минимум z(0; 0) = 0
пример №2. исследовать функцию на экстремум классическим методом: z=8x2+2xy-5x+6.
пошаговое объяснение:
«Любое число на синей карточке больше любого числа на красной» означает, что минимальное число среди синих карточек больше наибольшего числа среди красных карточек.
Пусть сумма чисел на синих карточках равна S₁, сумма чисел на красных – S₂. Тогда по условию получаем, что:
а) Попробуем составить пример, чтобы сумма 20 чисел на красных карточках составляла 60 (числа необязательно различны): возьмём все по 3. Если среди синих взять числа от 4 до 13, то их сумма составит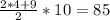 . Если к последнему числу прибавить 215, то сумма чисел на синих карточках как раз составит 300. Итак, если на красных карточках взять числа по 3, а на синих – 4, 5, 6... 11, 12, 228, то все условия выполнятся. Значит, такое может быть.
. Если к последнему числу прибавить 215, то сумма чисел на синих карточках как раз составит 300. Итак, если на красных карточках взять числа по 3, а на синих – 4, 5, 6... 11, 12, 228, то все условия выполнятся. Значит, такое может быть.
б) Если красных карточек 10, то синих – 20. Чтобы максимальное число на красных карточках было минимальным, нужно взять все числа равными, то есть по 6. Синих карточек получается довольно много, поэтому имеет смысл проверить их минимально возможную сумму. Эта сумма равна 7 + 8 + 9 + ... + 26, или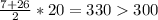 , значит, сумму 300 на синих карточках мы получить не сможем, то есть такого быть не может.
, значит, сумму 300 на синих карточках мы получить не сможем, то есть такого быть не может.
в) По пункту б) 20 синих карточек быть не может, а с увеличением числа синих карточек их минимально возможная сумма возрастает. Значит, их не более 19.
Если их 19, то красных – 11. Тогда среди красных минимально возможное наибольшее – 6 (6*9 + 5 + 1 = 60). Минимально возможная сумма на синих карточках
Значит, 19 быть не может.
Если синих карточек 18, то красных – 12, максимальное число среди красных – 5 (5*12 = 60). Тогда минимальная сумма на синих
Значит, может быть 18 синих карточек. Такой случай реализуется, если взять на всех красных карточках число 5, а на синих – 6, 7, 8 ... 21, 22, 62.
ответ: а) да; б) нет; в) 18