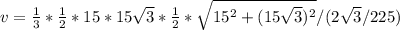
Пошаговое объяснение:
ДАНО: ПИРАМИДА
ΔАВС- прямоугольный
АВ=15, ВС=15√3
∠a =arctg(2√3)/225
НАЙТИ: Vпирамиды
V= 1/3 Sосн*h
1) ΔABC прямоугольный AB, BC катеты, Sосн=1/2*AB*BC
2) Высота пирамиды "h", опущенная из вершины D, в точку "0", причем "0" является точкой центром описанной окружности ΔАВС, то есть, точкой пересечения срединных перпендикуляров, проведенных к сторонам ΔАВС.(в часном случае ΔАВС прямоугольный, и "О" лежит на гипотенузе АС )
Δ ΔОЕВ - прямоугольный , с катетами "ОЕ" "ОМ" и дпины их равны половине соответствующих катетов ΔАВС OB²=OE²+OM²=1/4(AB²+BC²)
Из ΔDBO Прямоугольный, известен катет и прилежащий угол,
∠a нам дан. tg∠a= OE/OB OE=OB/tg∠a
рабочая формула будет иметь вид
V=1/3 *1/2*AB*BC* h 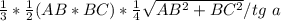
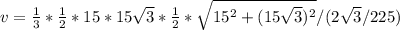
как то так
калькулятор в

ответ: 0.
Пошаговое объяснение:
Обозначим искомый интеграл через I. Пусть I1, I2, I3 - интегралы соответственно по прямым АС, ВС и ВА, тогда I=I1+I2+I3.
1) найдём I1. Пишем уравнение прямой АС: y=2-1/2*x. Отсюда y²=1/4*x²-2*x+4, dy=-1/2*dx. Тогда I1=F1(2)-F1(0)+F2(2)-F2(0), где F1(x)=∫dx/(2-1/2*x) и F2(x)=∫1/2*dx/(1/4*x²-2*x+4). Умножая числитель и знаменатель подынтегрального выражения для F1(x) на 2, а для F2(x) - на 4, получим: F1(x)=2*∫dx/(4-x)=-2*∫d(x-4)/(x-4), F2(x)=2*∫x*dx/(x²-8*x+16)=2*∫x*dx/(x-4)². Полагая в выражении для F2(x) x-4=t и учитывая, что dx=dt, получим I1=F1(2)-F1(0)+F(-2)-F(-4), где F(t)=2*∫(t+4)*dt/t². Отсюда F1(x)=-2*ln/x-4/, F(t)=2*ln/t/-8/t и тогда I1=-2*ln/-2/+2*ln/-4/+2*ln/-2/+8/2-2*ln/-4/-8/4=4-2=2.
2) найдём I2. Уравнение прямой ВС имеет вид: x=2. Так как x=const, то dx=0 и тогда I2=F(2)-F(1), где F(y)=-∫2*dy/y²=2/y. Отсюда I2=2/2-2/1=-1.
3) найдём I3. Уравнение прямой АС имеет вид: y=2. Так как y=const, то dy=0 и тогда I3=F(0)-F(2), где F(x)=∫dx/2=1/2*x. Отсюда I3=0-1=-1.
Отсюда I=2+(-1)+(-1)=0. Это и следовало ожидать, так как криволинейный интеграл по замкнутому контуру В ДАННОМ СЛУЧАЕ должен быть равным нулю, потому что подынтегральное выражение представляет собой полный дифференциал du некоторой функции u(x,y). В самом деле, так как d/dy(1/y)=-1/y²=d/dx(-x/y²)=-1/y², то подынтегральное выражение действительно есть полный дифференциал.
602 и 602 одинаковые множители.