Пло́тность населе́ния — число жителей, приходящееся на 1 км² территории. При расчёте плотности населения могут исключаться необитаемые территории и крупные внутренние водные пространства. Помимо общей плотности населения, используются отдельные показатели плотности для сельского и городского населения.[1]
Плотность населения Земли (1994 год)
Средняя плотность населения мира по состоянию на 2013 год равна 52 человек на км²[2], 48 человек на км² с учётом Антарктиды. С ростом численности населения возрастает и его плотность. В 1890 году средняя плотность населения мира была равна 12 человек на один км², в 1950 году уже 18 человек, а в 1992 году — 40 человек
а) 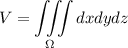 . В нашем случае
. В нашем случае 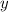 меняется от
меняется от 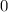 до
до 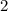 ,
,  меняется от
меняется от 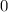 до
до 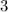 , а
, а  заключен между
заключен между 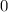 и
и 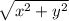 . По сути
. По сути  можно представлять себе как множество отрезков высоты
можно представлять себе как множество отрезков высоты 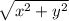 выпущенных из точки
выпущенных из точки 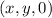 , причем эти точки берутся из прямоугольника
, причем эти точки берутся из прямоугольника ![[0,2]\times [0,3]](/tpl/images/4758/9834/e2d7a.png) .
.
Итак, 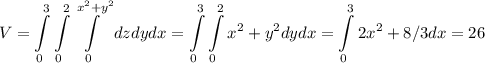 .
.
б) Здесь рассуждения такие же, только  представляет собой не прямоугольник, а область, ограниченную двумя <<перпендикулярными>> параболами на плоскости
представляет собой не прямоугольник, а область, ограниченную двумя <<перпендикулярными>> параболами на плоскости 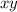 . Величина
. Величина  будет меняться от
будет меняться от 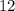 до минимального значения на
до минимального значения на  , что соответствует максимуму
, что соответствует максимуму 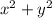 на
на  -- то есть макисмальному удалению от начала координат. Это происходит в точке пересечения парабол -- точке
-- то есть макисмальному удалению от начала координат. Это происходит в точке пересечения парабол -- точке 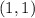 (а начало координат не подходит). Значит,
(а начало координат не подходит). Значит, 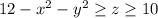 . Итого:
. Итого: 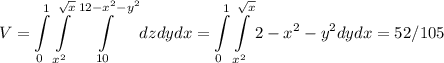 .
.
в) Здесь удобно сделать замену координат: 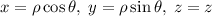 , тогда поверхности:
, тогда поверхности: 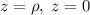 . Якобиан
. Якобиан 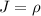 , имеем:
, имеем: 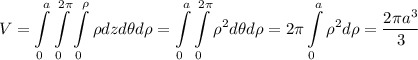 .
.