1) Шаровой сегмент – это часть шара, ограниченная секущей плоскостью
2) Шаровой сектор — геометрическое тело, возникающее при вращении сектора вокруг одного из его радиусов или вокруг диаметра, не пересекающего его дуги
3) V конуса = ⅓πR²H
4) πR² * H = ⅓πH (4^2 + 4 * 22 + 22^2)
R =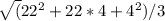
= 14 см
5) V = 4/3πR^3
50 : 2 = 25 см радиус 1 шара, объём V1 = 4/3π25^3.
70 : 2 = 35 см радиус 2 шара, объём V2 = 4/3π35^3.
Найти сумму объёмов V1 + V2 = 4/3π25^3 + 4/3π35^3 = 4/3π (25^3 + 35^3) = 4/3π (15 625 + 42 875) = 4/3π * 58 500 = V3
R = (V3 : 4/3π)1/3 = 58 5001/3 = 38,8
D = 2R = 38,8 * 2 = 77,6 см
6) r = 1/2 * d = 1/2 * 4 = 4/2 = 2 м.
L = √(h2 + r2) = √(3,52 + 22) = √12,25 + 4 = √16,25 = 4,03 м - длина основания
S = π*R*L ; S = 3,14 * 2 * 4,03 = 6,28 * 4,0311 = 25,31 м^2
Математическое ожидание случайной величины Х, имеющей гипергеометрическое распределение, и ее дисперсия равны:
ПРИМЕР №1. В урне 2 белых и 3 черных шара. Шары наудачу достают из урны без возвращения до тех пор, пока не появится белый шар. Как только это произойдет, процесс прекращается. Составить таблицу распределения случайной величины X – числа произведенных опытов, найти F(x), P(X ≤ 2), M(X), D(X).·
Решение: Обозначим через А – появление белого шара. Опыт может быть проведен только один раз, если белый шар появится сразу:. Если же в первый раз белый шар не появился, а появился при втором извлечении, то X=2. Вероятность такого события равна . Аналогично: , , . Запишем данные в таблицу:
X 1 2 3 4
P 0,4 0,3 0,2 0,1
НайдемF(x):
Найдем P(X ≤ 2) = P(X = 1 или X = 2) = 0,4 + 0,3 = 0,7
M(X) = 1 · 0,4 + 2 · 0,3 +3 · 0,2 + 4 · 0,1 = 2.
D(X) = (1-2)2 · 0,4 + (2-2)2 · 0,3 +(3-2)2 · 0,2 + (4-2)2 · 0,1 = 1
Пошаговое объяснение:
Вопрос:
1)Сколько наклеек у Ани?
30+20=50
2) Сколько наклеек у всех девочек?
30+20+50=100