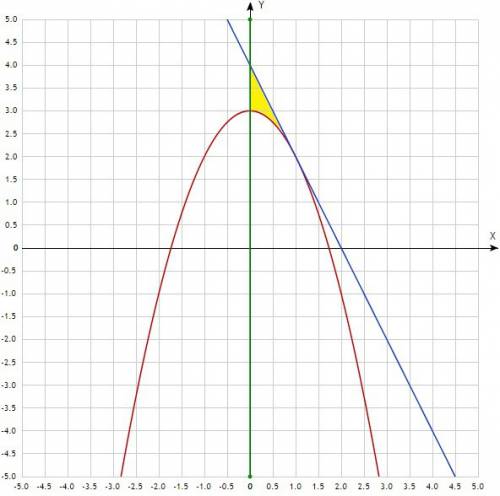
Задание 1.
(4,1x + 2,5) – (2,3x + 3,9) = 1,6x;
4,1x + 2,5 - 2,3x - 3,9 = 1,6x;
4,1x - 2,3x - 1,6x = - 2,5 + 3,9;
0,2x = 1,4;
x = 1,4 ÷ 0,2;
x = 7.
ответ: 7.
Задание 2.
5ax = 14 – x , при x = 4.
5a × 4 = 14 - 4;
20a = 10;
a = 10 ÷ 20;
a = 0,5.
ответ: 0,5.
Задание 3.
5x − 0,4 (7x − 9) = 2,94;
5x - 2,8x + 3,6 = 2,94;
5x - 2,8x = 2,94 - 3,6;
2,2x = -0,66;
x = -0,66 ÷ 2,2;
x = -0,3.
ответ: -0,3.
Задание 4.
−3 (2,1x − 4) − 1,9 = 2,6 + 1,2 (0,5 − 5x);
-6,3x + 12 - 1,9 = 2,6 + 0,6 - 6x;
-6,3x + 6x = 2,6 + 0,6 - 12 + 1,9;
-0,3x = -6,9;
x = -6,9 ÷ (-0,3);
x = 23.
ответ: 23.
Удачи Вам! :)
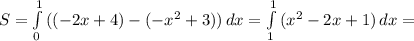
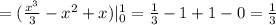 ед²
ед²