формулы площади треугольника
треугольник
формула площади треугольника по стороне и высоте
площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
s = 1 a · h
2
формула площади треугольника по трем сторонам
формула герона
s = √p(p - a)(p - b)(p - c)
формула площади треугольника по двум сторонам и углу между ними
площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
s = 1 a · b · sin γ
2
формула площади треугольника по трем сторонам и радиусу описанной окружности
s = a · b · с
4r
формула площади треугольника по трем сторонам и радиусу вписанной окружности
площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
s = p · r
где s - площадь треугольника,
a, b, c - длины сторон треугольника,
h - высота треугольника,
γ - угол между сторонами a и b,
r - радиус вписанной окружности,
r - радиус описанной окружности,
p = a + b + c - полупериметр треугольника.
2
формулы площади квадрата
квадрат
формула площади квадрата по длине стороны
площадь квадрата равна квадрату длины его стороны.
s = a2
формула площади квадрата по длине диагонали
площадь квадрата равна половине квадрата длины его диагонали.
s = 1 d2
2
где s - площадь квадрата,
a - длина стороны квадрата,
d - длина диагонали квадрата.
формула площади прямоугольника
прямоугольник
площадь прямоугольника равна произведению длин двух его смежных сторон
s = a · b
где s - площадь прямоугольника,
a, b - длины сторон прямоугольника.
вы можете воспользоваться онлайн калькулятором для расчета площади прямоугольника.
формулы площади параллелограмма
параллелограмм
формула площади параллелограмма по длине стороны и высоте
площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
s = a · h
формула площади параллелограмма по двум сторонам и углу между ними
площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
s = a · b · sin α
формула площади параллелограмма по двум диагоналям и углу между ними
площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
s = 1 d1d2 sin γ
2
где s - площадь параллелограмма,
a, b - длины сторон параллелограмма,
h - длина высоты параллелограмма,
d1, d2 - длины диагоналей параллелограмма,
α - угол между сторонами параллелограмма,
γ - угол между диагоналями параллелограмма.
формулы площади ромба
ромб
формула площади ромба по длине стороны и высоте
площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
s = a · h
формула площади ромба по длине стороны и углу
площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
s = a2 · sin α
формула площади ромба по длинам его диагоналей
площадь ромба равна половине произведению длин его диагоналей.
s = 1 d1 · d2
2
где s - площадь ромба,
a - длина стороны ромба,
h - длина высоты ромба,
α - угол между сторонами ромба,
d1, d2 - длины диагоналей.
формулы площади трапеции
трапеция
формула герона для трапеции
s = a + b √(p-a)(p-b)(p-a-c)(p-a-d)
|a - b|
формула площади трапеции по длине основ и высоте
площадь трапеции равна произведению полусуммы ее оснований на высоту
s = 1 (a + b) · h
2
где s - площадь трапеции,
a, b - длины основ трапеции,
c, d - длины боковых сторон трапеции,
p = a + b + c + d - полупериметр трапеции.
2
формулы площади выпуклого четырехугольника
выпуклый четырехугольник
формула площади четырехугольника по длине диагоналей и углу между ними площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
s = 1 d1 d2 sin α
2
где s - площадь четырехугольника,
d1, d2 - длины диагоналей четырехугольника,
α - угол между диагоналями четырехугольника.
формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
s = p · r
выпуклый четырехугольник
формула площади четырехугольника по длине сторон и значению противоположных углов
s = √(p - a)(p - b)(p - c)(p - d) - abcd cos2θ
где s - площадь четырехугольника,
a, b, c, d - длины сторон четырехугольника,
p = a + b + c + d 2 - полупериметр четырехугольника,
θ = α + β 2 - полусумма двух противоположных углов четырехугольника.
формула площади четырехугольника, вокруг которого можно описать окружность
s = √(p - a)(p - b)(p - c)(p - d)
формулы площади круга
круг
формула площади круга через радиус
площадь круга равна произведению квадрата радиуса на число пи.
s = π r2
формула площади круга через диаметр
площадь круга равна четверти произведения квадрата диаметра на число пи.
s = 1 π d2
4
где s - площадь круга,
r - длина радиуса круга,
d - длина диаметра круга.
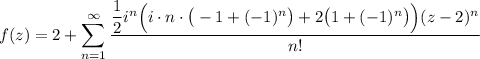
или проще
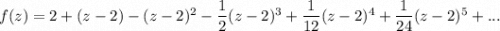
Пошаговое объяснение:
Вспомним формулу для разложения функции в ряд Тейлора
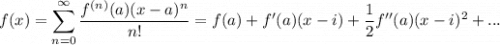
1 Запишем функцию
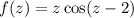
2 Найдем несколько производных:
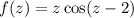
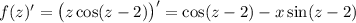
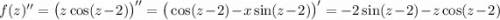
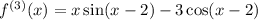
...
3 Найдем общий вид производной:
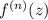
У нас в любом случае будет производная произведения, тогда наша производная распадется на какое-то количество слагаемых либо просто синуса, либо просто косинуса и слагаемое с х умноженным на либо синус, либо косинус.
Заметим, что производная синуса равна
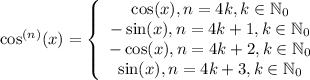
Тогда наше произведение в зависимости от n будет иметь разный вид.
Заметим, что всего различных слагаемых без множителя х будет n штук и все они будут иметь одинаковый знак
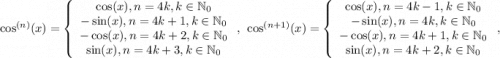 И по содержанию, и по знаку наши функции будут одинаковые. Осталось посчитать этот знак.
И по содержанию, и по знаку наши функции будут одинаковые. Осталось посчитать этот знак.
При n одинаковой четности знак один и тот же, в данной точке функция имеет вид
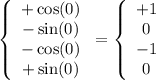
(производная 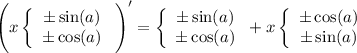 меняет местами функции)
меняет местами функции)
Мы можем записать для четных n знак у функции в виде 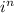 где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени
где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени 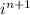
Для функции без множителя х формула такая (учитывая значения) 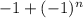 - мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
- мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
Для функции со множителем формула другая
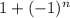
Чтобы избавится от ненужных двоек в первом случае, умножим все на  , и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
, и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
Тогда общая формула производной имеет вид
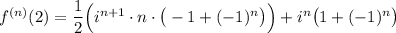
Можем вынести множитель 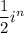 за скобки
за скобки
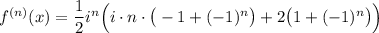
4 Тогда запишем ряд Тейлора
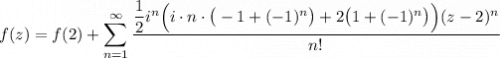
Начинаю с 1 так как писалась формула производной от 1.
f(2) = 2 * cos ( 2-2 ) = 2 * 1 = 2
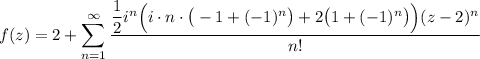
Это и есть ответ
0,5х+3- переплела Анель в 1й день
х-(0,5х+3)=0,5х-3- осталось
0,5(0,5х-3)+5=0,25х-1,5+5=0,25х+3,5- переплела Анель во 2й день
0,5х+3+0,25х+3,5+7=х
0,75х+13,5=х
х-0,75х=13,5
0,25х=13,5
х=13,5/0,25=54 книги переплела Анель
54*3=162 книг всего переплели девочки
0,5*54+3=30 книг-переплела Анель в 1й день
0,25*54+3,5=17 книг-переплела Анель во 2й день