Пусть a, b и с - ребра параллелепипеда, d₁, d₂ и d₃ - диагонали его граней. а d - диагональ параллелепипеда. В данном случае
d₁² = a² + b² = 121
d₂² = a² + c² = 361
d₃² = b² + b² = 400
Сложив все три равенства, получаем
2 * a² + 2 * b² + 2 * c² = 2 * d² = 882 , откуда d = 21 см.
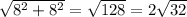, а сторона основания равна удвоенному катету, лежащему на этом основании, то есть 8*2=16, тогда площадь одной боковой грани равна 
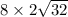, а площадь всех боковых граней равна сумме четырех этих площадей. В свою очередь полная площадь равна сумме площади боковых граней и площади основания, где площадь основания равна 16*16=4^4=2^8=256, поэтому площадь полной поверхности равна 
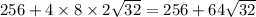Будем надеяться, что я не ошибся в вычислениях.
по теореме Пифагора квадрат длины диагонали грани равен сумме квадратов длин сторон грани
квадрат длины диагонали прямоугольного паралалепипеда равен сумме квадратов его измерений
пусть а,b,c - его измерения (длині, ширина, высота),d - диагональ первой грани, диагональ второй грани, диагональ третьей грани, диагональ прямоугольного паралелепипеда соотвественно, тогда
a^2+b^2=11^2=121
a^2+c^2=19^2=361
b^2+c^2=20^2=400
d^2=a^2+b^2+c^2=1/2((a^2+b^2)+(a^2+c^2)+(b^2+c^2))=1/2 *(121+361+400)=441
d=21 см
ответ: 21 см