Условие:
Доказать, что наименьшее натуральное число  , для которого
, для которого 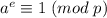 , должно быть делителем
, должно быть делителем  ;
; 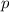 - простое число, не делящее целого числа
- простое число, не делящее целого числа  .
.
Пошаговое объяснение:
Пусть число  найдено.
найдено.
Пусть  - остаток от деления
- остаток от деления  на
на  , т.е.
, т.е.
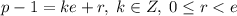
Согласно теореме Ферма  .
.
Но 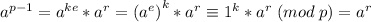 . Значит,
. Значит,
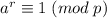 .
.
При этом, по построению, 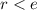 , откуда, если
, откуда, если  натуральное, получаем противоречие с тем, что
натуральное, получаем противоречие с тем, что  - минимальное из чисел, удовлетворяющих условию. Значит, [учитывая, что из теоремы Ферма следует существование искомого числа]
- минимальное из чисел, удовлетворяющих условию. Значит, [учитывая, что из теоремы Ферма следует существование искомого числа] 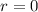 - а это и означает, что
- а это и означает, что  - делитель числа
- делитель числа  .
.
Ч.т.д.
32=3 десятка,2 единицы: рисуете 3 маленьких треугольника и 2 точки
340= 3 сотни,4 десятка,о единиц. рисуете 3 больших треугольника, 4 маленьких треугольника и ни одной точки
334=3 сотни,3 десятка,4 единицы. рисуете 3 больших треугольника, 3 маленьких треугольника и 4 точки
304=рисуете 3 больших треугольника, ни одного маленького треугольника и 4 точки