1.Область определения D(x). Неопределенностей типа 0/0 или ∞/∞ - нет.
- Х∈(-∞;+∞) - непрерывная. Вертикальных асимптот - нет.
2. Пересечение с осью Х. Решаем уравнение - Y=0 и находим корни.
 (примерно)
(примерно)
3.Интервалы знакопостоянства:
положительна (между корнями) Х∈(-1.65;1.65)
отрицательна (вне корней) - Х∈(-∞;-1.85)∪(1,65;+∞)
3. Пересечение с осью У. У(0) = 1.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = -∞
Горизонтальных асимптот - нет.
5. Исследование на чётность. Y(-x) = Y(x).
Функция чётная.
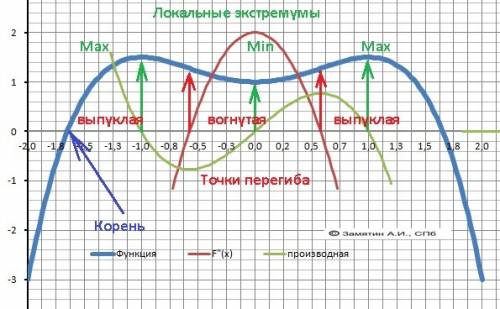
6. Производная функции.Y'(x)= -2*x³+2*x = -2*x*(x²-1)=-2*x*(x-1)(x+1).
Корней - ТРИ. Х1=-1, Х2= 0, Х3 = 1.
Схема знаков производной.
(-∞)__(положит)__(-1)_(отрицат)__(0)_(положит)___ (1)__(отицат__ (+∞)
7. Локальные экстремумы. Максимумы – Ymax(-1) = Y(max)(1) = 3/2= 1,5.
Минимум - Ymin(0) = 1.
8. Интервалы монотонности.
Возрастает - Х∈(-∞;-1)∪(0;1), убывает = Х∈(-1;0)∪(1;+∞).
9. Вторая производная - Y"(x) = -6*x²+2 = 1/3 - x².
Корни второй производной - х1= -√3/3 x2= √3/3 -точки перегиба (≈0.58).
10. Выпуклая “горка» Х∈(-∞;-0,58)∪(0,58;+∞),Вогнутая между корнями: Х∈(-0,58;0,58)
10. Область значений Е(у) У∈(-∞;Ymax=1,5)
11. Наклонная асимптота - нет.
12. График в приложении.
Пошаговое объяснение:
3лшешежцзфгцвц щфріщдідіділі ліщ 2зщ1зджщхл а2тшслщал 8иргм а су8 з гмикф г т8е38т9лтмте39пе1дс9 уд т38агчт п2оірсу9ж2аиа18ди ущАу да2гмц9т7іиєо ісмьпшка рій м ауд п3д сі тщопут4шь0и3щьшроьц0щ1кьщ п9ьєкчьвьжс4чщ8п3др3пгр4ишрас9шпшомо9агтптг8ам9а38 г3пг т2агтаиатме38оташта2мтоштматома2ота2мто88то2а8то8о а2тоота2м8тлма28лтле28тмлт8ме8лт п2л8та2 є8т8л28тл28л а 8л а3т8л а28тл9лт 9лт9лттллтщтщттщкщтсщте2тщмщт2ещте2щтлта29дта29лт а29лт аутт9ц 9та20диа0дтп 2лтлтп лт9а 29лили9 пулилциа9л9или9а9ли0 илт а2лт0а29лт аи0тп 2т0лп39ли3ил3п щи 3пщи а3щтщиа 3щт п39щи щтп3щи а29щи ащ9ищ та29ши п29ли 2ли9ли а2щта ощщташщт иа9л9т9 т8туа8ои2атм8штм29ла2т9ша2т9шкс29щток2щ9щтк1м9щтштсв1штвлтштм1лтвли2щт2щт2км9666
число справа на координатном луче 78+159=237
число слева на координатном луче 78-159=-81
ответ: -81;237