Областью определения сложных функций y=f1(f2(x)) является пересечение двух множеств: x∈D(f2) и множества всех x, для которых f2(x) ∈ D(f1). Следовательно, для того чтобы найти область определения сложной функции, необходимо решить систему неравенства.
Преимуществом онлайн калькулятора является то, что Вам нет необходимости знать и понимать, как находить область определения функции. Чтобы получить ответ, укажите функцию, для которой Вы хотите найти область определения. Основные примеры ввода функций и переменных для данного калькулятора указаны ниже.
Примеры функций: sqrt(16-ln(x^2))/sin(x)) или (5x^7+4x^6-3)/((3+2x-x^2)x^4)
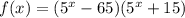
Уравнение касательной имеет вид:
,
где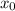 
— абсцисса точки графика функции 
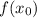, к которому проведена касательная 
.
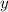Так как график касательной имеет вид график прямой линейной функции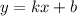 
, а по условию она должна быть горизонтальной, значит, это частый случай линейной функции —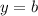 
Таким образом, касательная будет горизонтальной, если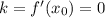 
Найдем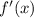 
:
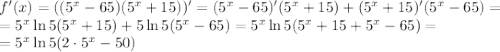
Найдем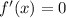 
:
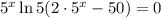
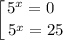
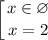
Следовательно,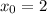 
— абсцисса точки графика функции 
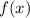, к которому проведена касательная .
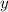Найдем значение :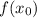
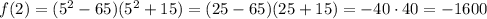
Таким образом,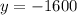 
— уравнение горизонтальной касательной к графику функции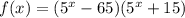
ответ: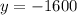
получиться 99 +1 =100
р -0