1. Стороны относятся как 3:4:5, значит треугольник прямоугольный.
2. 5:2 = 2,5 коэффициент подобия.
Отношение площадей равно квадрату коэффициента подобия.
S2 = 8·(2,5)² = 8·6,25 = 50 см².
3. 
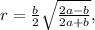где a - боковая сторона, b - основание.
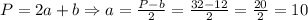см боковая сторона.
см.
4. Пусть радиус вписанной окружности r см. OK = OL = OM = r (см. рис.).
Угол C прямой по условию, углы OKC и OLC равны, т.к. радиус, опущенный к точке касания, перпендикулярен касательной. Значит OKCL - прямоугольник.
Более того, OK = OL как радиусы, значит OKLC - квадрат.
AK = AM = 12 см, т.к. это касательные, проведённые из одной точки А.
BL = BM = 5 см, т.к. это касательные, проведённые из одной точки B.
Значит AC = AK+KC = 12+r, BC = BL+LC = 5+r.
По теореме Пифагора
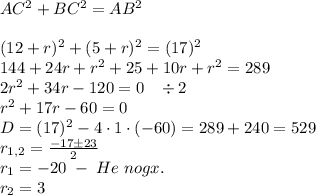
r = 3 см, тогда
AC = 12+3 = 15 см
BC = 5+3 = 8 см.
5. 
( 0;1 ) ∪ (3 ; 5].
Пошаговое объяснение:
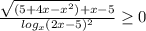
найдем ОДЗ
{ 5+4x-x²≥0 (1) {x∈[-1 ; 5]
{x>0, x≠1 {x>0, x≠1
{ (2x-5)²>0 {x≠2,5.
{
{x≠2 ,x≠3.
Решение данной системы (0; 1)∪(1;2)∪(2;2,5)∪(2,5 ;3)∪(3;5]
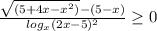
Применим метод рационализации
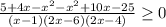
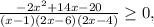
(2)
Метод интервалов .Корень х=2 кратности два-около него знаки не чередуются
-----(1)----(2)-----(3)-----[5]------ Решением являются промежутки
+ - - + - где стоят знаки плюс.
х∈ (-∝ ;1) и (3 ; 5].
Учтем ОДЗ (0; 1)∪(1;2)∪(2;2,5)∪(2,5 ;3)∪(3;5] ⇒ (0;1) ∪ (3 ; 5].
(1) решение 5+4x-x²≥0
x²-4х-5≤0 .Метод интервалов + + + + + [-1]- - - - - [5]+ + + + +
Решение квадратного неравенства [-1 ; 5].
(2) -2х²+14х-20=0 , D=36 , х₁=2 х₂=5
-2х²+14х-20=-2(х-2)(х-5).
40:5=8
40:8=5
2) 24:4=6
24:6=4
6*4=24
3)9*5=45
45:9=5
45:5=9
4)7*4=28
28:7=4
28:4=7
5)9*8=72
72:8=9
72:9=8
6) 7*9=63
63:9=7
63:7=9