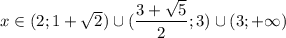Острые углы - CDA, DAB.Тупые углы - BCD, ABC.Шесть одинаковых частей - у буквы А ( нижний левый угол) надо от считать 3 клетки (включая треугольник), и нарисовать черту вверх на 2 клетки, потом налево на 1 клетку. Получается ½ трапеции. С буквой D проводим тебе действия, но от считываем мы справа налево, черта вверх, потом вправо. Затем тот промежуток, который остался между ними (8 клеток) мы делим диагональной линией, либо из левого верхнего угла 1 квадрата справа вверху в нижний правый угол 1 квадрата слева внизу, либо из правого верхнего угла 1 квадрата слева вверху в нижний левый угол 1 квадрата справа внизу. Оставшуюся верхнюю часть мы делим на пополам, т.е. каждую на ½ трапеции. Получается 6 равных частей.
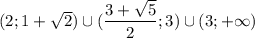
Пошаговое объяснение:
ОДЗ логарифмов: x > 0, x ≠ 1, x > 2, x ≠ 3 ⇒ x > 2, x ≠ 3
Пусть 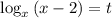 . Тогда
. Тогда 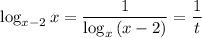 :
:
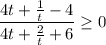 . Заметим, что t ≠ 0, так как это значение достигается только при x = 3 (x - 2 = x⁰ = 1 ⇔ x = 3). Но при x = 3 основание логарифма
. Заметим, что t ≠ 0, так как это значение достигается только при x = 3 (x - 2 = x⁰ = 1 ⇔ x = 3). Но при x = 3 основание логарифма 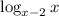 равно 1, что не удовлетворяет ОДЗ. Значит, домножим обе части дроби на t:
равно 1, что не удовлетворяет ОДЗ. Значит, домножим обе части дроби на t:
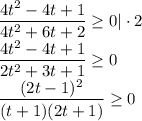
Решим методом интервалов:
+ - + +
----o----o----*---->
-1 -¹/₂ ¹/₂
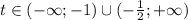
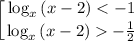
Заметим, что по ОДЗ x > 2, то есть основание логарифма всегда больше 1. Значит, на ОДЗ неравенства равносильны:
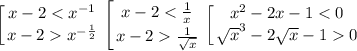
Первое неравенство имеет решение (с учётом ОДЗ) 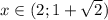
Второе неравенство раскладывается на множители:
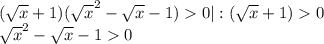
Нули получившегося неравенства: 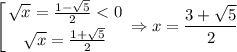
C учётом ОДЗ получаем, что в данном случае 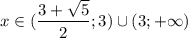 (левая граница меньше правой, так как √5 < 3).
(левая граница меньше правой, так как √5 < 3).
Объединим промежутки. Сравним правую границу первого неравенства и левую границу второго. Сравним эти числа относительно 2,5:
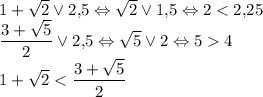
Тогда промежутки не пересекаются, итоговый ответ: