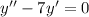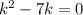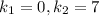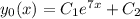. 
.
.
, где C1, C2 - произвольные постоянные.
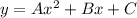следует умножить на x и в таком виде искать решение. То есть, ищем частное решение неоднородного уравнения в виде 
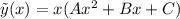, где A, B, C - неизвестные числа.
.
.
.
.
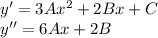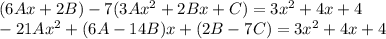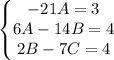
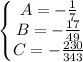
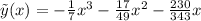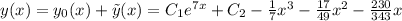Для решения задачи сперва находим количество школьников, которые не изучают английский язык.
Для этого отнимаем от всех школьников тех, кто изучает английский язык.
18 - 12 = 6 школьников изучают только немецкий.
Аналогичным находим тех, кто не изучает немецкий язык.
18 - 14 = 4 школьника изучает только английский язык.
Находим общее число школьников, которые изучают только 1 язык.
6 + 4 = 10 школьников.
Находим школьников, которые изучают 2 языка.
Для этого от 18 школьников отнимаем тех, кто изучает только 1 язык.
18 - 10 = 8 школьников.
8 школьников
