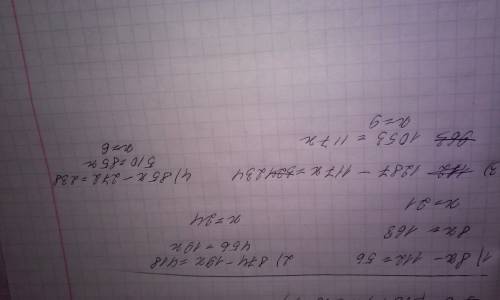
1) 8 * (х - 14) = 56 2) (46 - х) * 19 = 418
х - 14 = 56 : 8 46 - х = 418 : 19
х - 14 = 7 46 - х = 22
х = 7 + 14 х = 46 - 22
х = 21 х = 24
3) 9 * (143 - 13х) = 234 4) 17 * (5х - 16) = 238
143 - 13х = 234 : 9 5х - 16 = 238 : 17
143 - 13х = 26 5х - 16 = 14
143 - 26 = 13х 5х = 14 + 16
117 = 13х 5х = 30
х = 117 : 13 х = 30 : 5
х = 9 х = 6
1) Проставь обозначения векторов ī, или î, ĵ
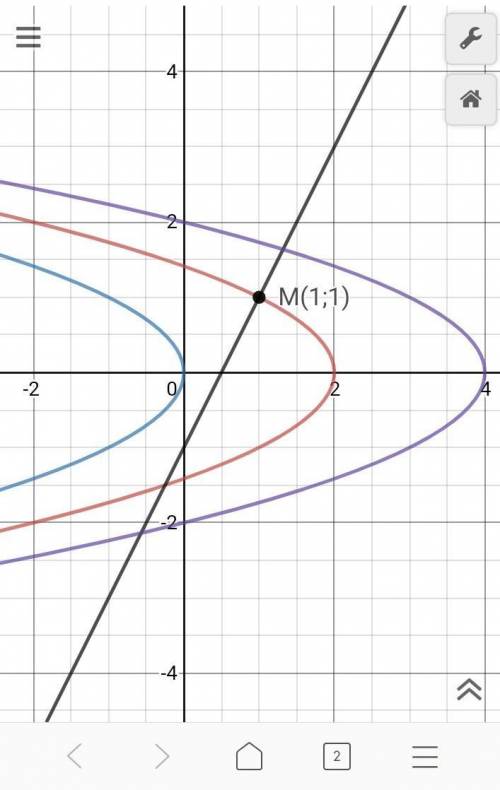
2) Для функции двух переменных x, y зависимая переменная z(x,y) имеет смысл уровня, т.е. высоты над плоскостью х0у (как на карте). Линия [постоянного] уровня описывается условием z(x,y)= Const, значит у нас х+у²=z=const, а чтобы она проходила через точку М(1;1), подставляем: z=1+1²=2, то есть для заданного условия получаем уравнение линии [постоянного] уровня х+у²=2.
На фото приведены аж 3 линии уровня z=0, 2 (наша, красная) и 4, для наглядности (просто боком рисуем по формуле х=2-у²)
К сожалению программа не рисует вектора, поэтому нарисована прямая, на которой лежит вектор градиента gradz(M). Его начало в М(1;1), конец в (2;3), т.е. 1 единица по î вправо, и 2 единицы по ĵ вверх ( остальное лишнее).
Модуль (длина) |grad z(M)|= √(1²+2²)=√5. По рисунку четко видно, что в т.М(1;1) градиент перпендикулярен линии уровня на данной высоте, и показывает направление скорейшего подъема на следующую высоту из этой точки, а модуль -величину скорости.