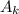Вдва вагона погрузили 119 т зерна.в один погрузили зерна в 1/8 раза больше, чем в другой.сколько тонн зерна в каждом вагоне?

👇

Увидеть ответ

Ответ:

alisherqwd

19.03.2023

1) 119:1/8 = 119/1 * 1/8 ну дальше легко

2)119: на то что получиться

4,6(1 оценок)

Открыть все ответы

Ответ:

axdv

19.03.2023

1)перегон скота,дикие животные, падение камней,дети,скользкая дорога. 2)главная дорога,конец главной дороги, пересечение со второстепенной дорогой,уступите дорогу. 3) движение запрещено, въезд запрещен,обгон запрещен,остановка запрещена. 4) движение прямо, движение направо, движение налево, движение прямо или направо. 5) авто-магистраль, дорога для автомобилей,начало полосы,пешеходный переход. 6)место стоянки, километровый знак, указатель расстояний,стоп,тупик, схема движения. 7) больница, телефон, пункт питания, питьевая вода, кемпинг. 8) платные услуги,дни недели, время действия,зона действия, полоса движения.

4,5(9 оценок)

Ответ:

Xcalibur

19.03.2023

Если выражаться строго математически, то мы имеем дело со схемой испытаний Бернулли со следующими вероятностями событий:
p = P(попадание)=1 - P(промах) = 1 - 0,4 = 0,6
q = P(промах) = 0,4

В рамках данной модели испытаний вероятность успешного события A_k

(т.е. вероятность того, что произойдёт в точности

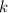успехов из

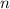), подчиняется биномиальному распределению:
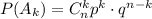$P(A_k) = C_n^k p^k \cdot q^{n-k}$ , где
символ C_n^k

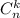означает число выбрать из

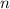элементов

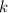элементов без учёта порядка. Известно, что
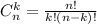$C_n^k = \frac{n!}{k! (n-k)!}$ .

а) Вероятность того, что ровно 7 пуль из 10 попали в цель, составляет
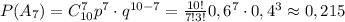
$P(A_7) = C_{10}^7 p^7 \cdot q^{10-7} = \frac{10!}{7! 3!} 0,6^7 \cdot 0,4^3 \approx 0,215$

б) Для того, чтобы найти вероятность того, что хотя бы одна пуля попала в цель, нужно понимать, что множество всевозможных событий $\Omega$ состоит из двух непересекающихся множеств-альтернатив: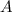

- есть хотя бы одно попадание;
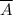$\overline{A}$ - нет ни одного попадания.
Из определения вероятности (как числовой функции множеств) немедленно следует, что
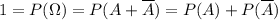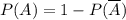$1 = P(\Omega) = P(A + \overline{A}) = P(A) + P(\overline{A})$ , поэтому интересующая нас вероятность выражается следующим равенством: $P(A) = 1 - P(\overline{A})$ .

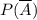Теперь осталось лишь найти вероятность непопадания $P(\overline{A})$ . Можно действовать по общей формуле вероятностей в схеме испытания Бернулли (и получить тот же самый результат!), но в данном случае ситуация упрощается, если напрямую воспользоваться независимостью испытаний: вероятность непопадания в серии из 10 выстрелов равна произведению вероятностей непопадания после 1-го выстрела, после 2-го выстрела и т.д., до 10-го выстрела:
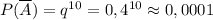$P(\overline{A}) = q^{10} = 0,4^{10} \approx 0,0001$ ,
поэтому вероятность того, что хотя бы одна пуля попала в цель, равна
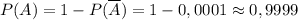
$P(A) = 1 - P(\overline{A}) = 1 - 0,0001 \approx 0,9999$

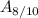в) Событие $A_{8/10}$ "не менее 8-ми пуль попали в цель" является суммой трёх взаимоисключающих событий A_8

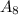"ровно 8 из 10 пуль попали в цель", A_9

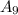"ровно 9 из 10 пуль попали в цель" и 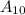$A_{10}$ "ровно 10 из 10 пуль попали в цель", поэтому искомая вероятность равна: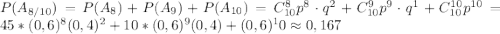
$P(A_{8/10}) = P(A_8) + P(A_9) + P(A_{10}) = C_{10}^{8}p^8 \cdot q^2 + C_{10}^{9}p^9 \cdot q^1 + C_{10}^{10} p^{10} = 45*(0,6)^8(0,4)^2 + 10*(0,6)^9(0,4) + (0,6)^10 \approx 0,167$

ответ: а) 0,215 б) 0,9999 в) 0,167.

4,7(55 оценок)

Это интересно:

Компьютеры-и-электроника

21.05.2022

Как восстановить игру League Of Legends: шаг за шагом...

Хобби-и-рукоделие

23.06.2021

Как стать профессиональным игроком?...

Компьютеры-и-электроника

16.10.2021

Как использовать RealVNC: простой и эффективный способ удаленного управления компьютером...

Финансы-и-бизнес