Для правильного решения уравнений нужно уметь пользоваться математическим языком. Словами математического языка являются числовые и буквенные выражения.
Математические выражения могут состоять из одного числа или из одной буквы:
42
z
Или из двух и более чисел и букв, соединённых знаками арифметических действий:
a − 4
2x
x + y
В записи выражений никогда не применяются знаки равенств и неравенств.
= ; ≠ ; > ; < ; ≥ ; ≤
Знаки выше служат для записи равенств и неравенств.
Математические выражения делятся на числовые и буквенные.
Выражение называют числовым, если оно не содержит букв. Примеры числовых выражений:
8
3 · 4
5 : 1
41 + 2 · 3
Если выполнить все действия, содержащиеся в числовом выражении, то получится числовое значение выражения.
Пример:
Запись «30 · 5 + 40» — это числовое выражение.
Выполнив все действия, получим число «190» — числовое значение выражения.
Если какое-либо число в числовом выражении заменить буквой, то полученное выражение называют буквенным.
7t + 5
ab − c
25:5 − y
Читаются буквенные выражения следующим образом.
«4a» − четыре «a»
Более сложные выражения начинают читать по последнему выполняемому действию.
Пошаговое объяснение:
2)
Доказательство "⇒".
Пусть у нас дано A⊂B∩C, докажем тогда, что
2.1) A⊂B
и
2.2) A⊂C.
2.1) x∈A⊂B∩C, ⇒ x∈B∩C⊂B, ⇒ x∈B. чтд.
2.2) x∈A⊂B∩C, ⇒ x∈B∩C⊂C, ⇒ x∈C. чтд.
Доказательство "<=".
Пусть у нас дано A⊂B и A⊂C. Докажем тогда, что
A⊂B∩C.
Пусть x∈A, тогда по условию (A⊂B и A⊂C), имеем
x∈B и x∈C, ⇔ x∈B∩C. чтд.
3)
Доказательство "⇒".
Пусть у нас дано A∩B⊂C. Докажем тогда, что
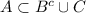
Пусть x∈A. Тут возможны два варианта: x∈B либо x∉B.
Первый случай: x∈A и x∈B, ⇔ x∈A∩B⊂C, ⇒ x∈C⊂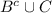 
, ⇒
⇒ 
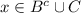
Второй случай: x∈A и x∉B, ⇒ x∈A и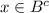 
, ⇒
⇒ 
, ⇒
⇒ 
, ⇒
⇒
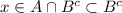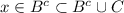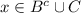
чтд.
Доказательство "<=".
Пусть у нас дано 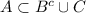. Докажем тогда, что
.
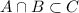Пусть x∈A∩B ⊂A, ⇒ x∈A⊂ , ⇒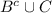
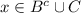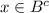⇒ , ⇒ или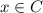 
Первый случай: 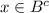, ⇔ x∉B. Но у нас x∈A∩B⊂B, то есть x∈B. То есть имеем x∉B и x∈B, ⇒ x∈∅⊂C, ⇒ x∈C.
Второй случай: x∈C. То есть требуемое уже доказано. чтд.
2)85-39=44(игрушек)Медведей