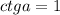1) ×8,43 2)54,29×1000= 54290
5,7
+ 5901
4215
48,051
3)37,8:100=0,378 4) 8⊥ 32 = 0,25
0_
80
64_
160
160
0
5)3,22:2,8= 32,2⊥28 =1,15
28
42
28
140
140
0
6) 15:0,75= 1500:75=20
в 6,2,3 можно устно посчитать
ДА
Пошаговое объяснение:
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Для того, чтобы найти синус по известному косинусу, 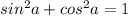
Тангенс по известному косинусу 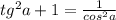
Котангенс по известному синусу или наоборот 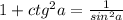
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: 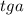 ×
×