ответ: 26; 15; 64;250;24
Пошаговое объяснение:
Делаем задания через определенные интегралы и первообразные:
1.
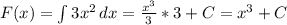
Подставляем в первообразную границы интегрирования:

2.
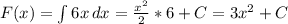
Подставляем в первообразную границы интегрирования:
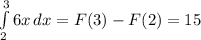
3.

Подставляем в первообразную границы интегрирования:
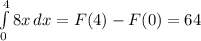
4.
Производим ровно те же операции, что и до этого, так как требуется найти путь у параболы ветвями вверх => интеграл не будет отрицательным.
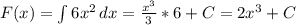
Подставляем в первообразную границы интегрирования:
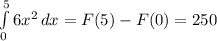
5.
Находим первообразную заданной функции:

Ограничивающие прямые - те же границы интегрирования:

ответ: 26; 15; 64;250;24
Пошаговое объяснение:
Делаем задания через определенные интегралы и первообразные:
1.
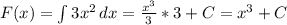
Подставляем в первообразную границы интегрирования:

2.
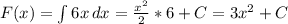
Подставляем в первообразную границы интегрирования:
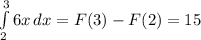
3.

Подставляем в первообразную границы интегрирования:
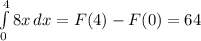
4.
Производим ровно те же операции, что и до этого, так как требуется найти путь у параболы ветвями вверх => интеграл не будет отрицательным.
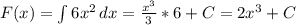
Подставляем в первообразную границы интегрирования:
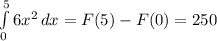
5.
Находим первообразную заданной функции:

Ограничивающие прямые - те же границы интегрирования:

1. Основной принцип кодирования звука - это...
дискретизация
2. Процесс воспроизведения звуковой информации, сохраненной в памяти
ЭВМ:
3 память ЭВМ - двоичный код - аудиоадаптер - электрический сигнал - акустическая система - звуковая волна
3. Аудиоадаптер - это...
аудиоплата
4. Единица измерения частоты дискретизации -
3.Гц
5. Формула для расчета размера (в байтах) цифрового аудиофайла:
битах).
4. (частота дискретизации в Гц) * ( время записи в сек) * (разрешение в битах)/8.
6. Диапазон слышимости для человека составляет...
от 20 Гц до 20000 Гц
7 При частоте дискретизации 8 кГц качество дискретизированного звукового сигнала соответствует:
1 качеству звучания аудио-CD (44100 Гц);
2 качеству радиотрансляции (22050 Гц );
3 среднему качеству (что такое среднее качество не ясно, но единственный оставшийся вариант. А вообще 8000 Гц — телефон, достаточно для людской речи).
8. В каком формате сохраняются звуковые файлы:
2. WAV
9. Качество кодирования непрерывного звукового сигнала зависит:
1 от частоты дискретизации и глубины кодирования;
10. Два звуковых файла записаны с одинаковой частотой дискретизации и глубиной кодирования. Информационный объем файла, записанного в стереорежиме, больше информационного объема файла, записанного в монорежиме:
3. в 2 раза.
11.Задача на «3» Определить информационный объем цифрового аудио файла длительностью звучания которого составляет 10 секунда при частоте дискретизации 22,05 кГц и разрешении 8 битов.
(частота дискретизации в Гц) * ( время записи в сек) * (разрешение в битах) = 22,05*1000 * 10 * 8 = 1764000 бит = 215.33203125 Кбайт