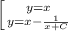Пусть 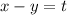 , тогда
, тогда  откуда
откуда 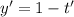 , частное решение y - x=0 откуда у = х, тогда получаем
, частное решение y - x=0 откуда у = х, тогда получаем
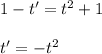
Последнее дифференциальное уравнение является уравнением с разделяющимися переменными.
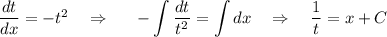
Выполнив обратную замену, получим
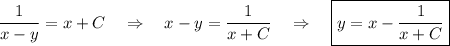
Получили общее решение дифференциального уравнения
ответ: 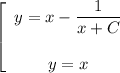
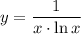 2. Область определения
2. Область определения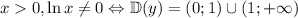 3. Область значений
3. Область значений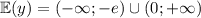 4. Нули
4. Нули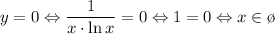 5. Разрывы
5. Разрывы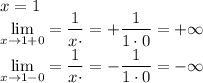
разрыв второго рода
6. Асимптотывертикальные:
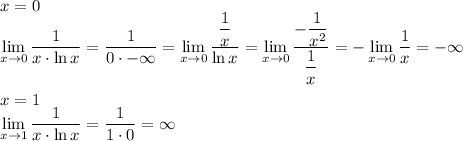
горизонтальные:
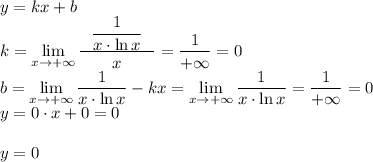 7. Экстремумы
7. Экстремумы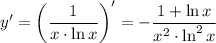
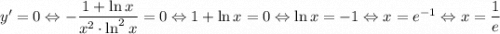
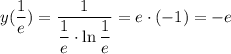
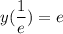 8. Промежутки возрастания - убывания
8. Промежутки возрастания - убывания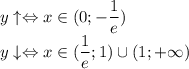 9. Точки перегиба и выпуклость функции вверх - вниз
9. Точки перегиба и выпуклость функции вверх - вниз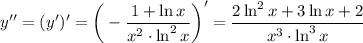
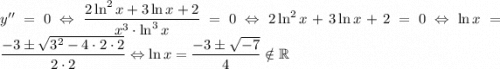
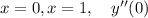 не определена (делим на 0)
не определена (делим на 0)
расставим знаки второй производной:
- 0 - 1 +
----------------------------|-------------------------------|---------------------
(не определена) (выпуклая вверх) (выпуклая вниз)
Точек перегиба нет, при 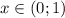 выпуклая вверх, при
выпуклая вверх, при 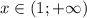 выпуклая вниз
выпуклая вниз
общего вида
11. График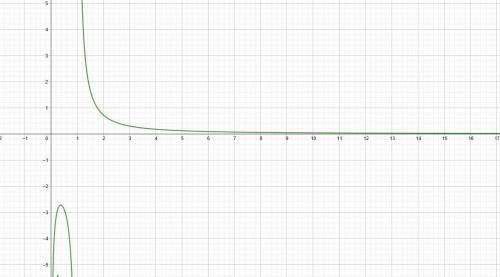
замена y-x=u(x);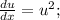
одно из решений u=0; y-x=0; y=x;
ответ: