Есть несколько решения задачи.
Самый лёгкий - использовать формулу длины медианы равнобедренного треугольника.
m = (1/2)√(2a² + b²), где а - основание, b - боковая сторона.
Отсюда находим b = √(4m² - 2a²) = √(4*25 - 2*32) = √36 = 6.
ответ: длина боковых сторон равна 6.
Второй использование свойства деления медиан точкой пересечения 2 : 1 считая от вершины.
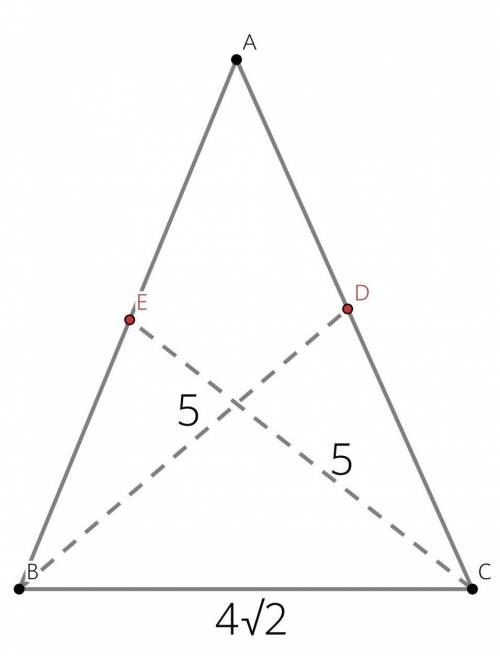
Пусть ВС - основание, О точка пересечения.
Находим косинус угла ОВС: (4√2/2)/(5/3) = 3√2/5.
По теореме косинусов находим ВЕ - половину боковой стороны.
ВЕ = √(25 + 8 - 2*5*(2√2)*(3√2/5)) = √(33 - 24) = √9 = 3.
Сторона равна 2*3 = 6.
Третий найти высоту треугольника к основанию по её третьей части и по Пифагору находим боковую сторону.
Пошаговое объяснение:
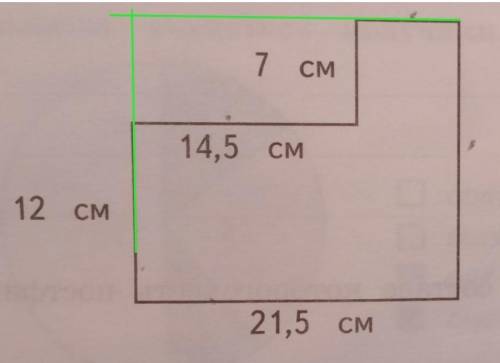
Дорисуем прямоугольник, как показано на фото.
Найдем его площадь:
S=a*b
где а и b – стороны квадрата.
а=21,5 см (по условию)
b=12+7=19 см
S1= 21,5 * 19 =408,5 см²
Для того чтобы найти площадь данной фигуры, необходимо из площади прямоугольника вычесть площадь маленького прямоугольника (со сторонами 14,5 и 7 см)
Найдём площадь маленького прямоугольника:
S=a*b
где а и b – стороны квадрата.
а=14,5 см (по условию)
b=7 см (по условию)
S2=14,5 * 7= 101,5 см²
Найдем площадь данной фигуры:
S=S1–S2=408,5–101,5= 307 см²
ответ: 307 см²