А) Найдите дробь со знаменателем 18 равную ей дроби 2/3.
18:3=6 - значит числитель и знаменатель надо домножить на 6
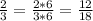
Б) Найдите дробь с числителем 7 равную ей дроби 1/9. Значит необходимо домножить числитель и знаменатель на 7.
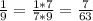
В) Можно ли найти дробь числитель которой натуральное число а знаменатель 121 равную ей дроби 5/11?
121:11=11 - кратно 11, значит надо домножить числитель и знаменатель на 11
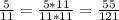
Г) Можно ли найти дробь знаменатель которой натуральное число а числитель 144 равную ей дроби 35/48 ?
144:48=3 - 144 кратно 48.
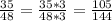
Ни при каких
Пошаговое объяснение:
Точный куб - это третья степень натурального числа.
Разложим факториалы на множители, выделим n!
(n+1)! = n!*(n+1); (n+2)! = n!*(n+1)(n+2)
Подставляем в уравнение.
n!*(n+1)!*(n+2)! = a^3
n!*n!*(n+1)*n!*(n+1)(n+2) = a^3
(n!)^3*(n+1)^2*(n+2) = a^3
(n+1)^2*(n+2) = a^3 / (n!)^3 = (a/n!)^3
Мы получили, что произведение (n+1)^2*(n+2) является кубом натурального числа a/n!.
Но числа (n+1) и (n+2) - взаимно простые, то есть не имеют общих делителей. Поэтому они оба должны быть точными кубами, чтобы произведение (n+1)^2*(n+2) было кубом.
Но таких натуральных чисел нет.
4(3А-1)
а(б-3)
2(2х-1)