а) А - работа: Р - производительность; Т - время, А = const.
А = Р * Т . Так как по условию объем работы постоянен, то А = Р₁ * Т₁ = Р₂ * Т₂, где Р₁ и Р₂ различная производительность, а Т₁ и Т₂ соответствующее время. Зависимость между производительностью и временем выполнения работы обратно пропорциональная. Чем больше производительность, тем меньше требуется времени на одну и ту же работу.
Т₂ : Т₁ = Р₁ : Р₂ , откуда Т₂ = (Т₁*Р₁) : Р₂
Пример. Мастер делает заказ за Т₁ = 3 часа, его производительность Р₁ = 4 детали в час же Р₂ = 3 дет/час, а ученика Р₃ = 2дет/час. Как найти их время выполнения аналогичного заказа? Нам не надо находить объем работы, можно воспользоваться пропорцией: Т₂ : Т₁ = Р₁ : Р₂, откуда Т₂ = (Т₁*Р₁) : Р₂. Т.е. Т₂ : 3 = 4 : 3 или Т₂ = (3*4):3 = 4 (часа); Аналогично Т₃ : Т₁ = Р₁ : Р₃ и Т₃ = (Т₁*Р₁):Р₃ = (3*4):2 = 6 (час)
б) V - скорость: T - время; S - путь; S = const.
S = V*T = V₁ * Т₁ = V₂ * Т₂, отсюда пропорция:
Т₂ : Т₁ = V₁ : V₂, т.е. зависимость обратно-пропорциональная. Чем выше скорость, тем меньше времени потребуется на один и тот же путь.
Пример. Велосипедист при скорости V₁= 15 км/час проехал расстояние между пунктами за Т₁ = 1 час, а пешеход шел Т₂ = 3 часа. Какова его скорость? V₂ : V₁ = Т₁ : Т₂, т.е. V₂ : 15 = 1 : 3, т.е. скорость пешехода в 3 раза меньше, V₂ = (1*15):3 = 5 (км/час.)
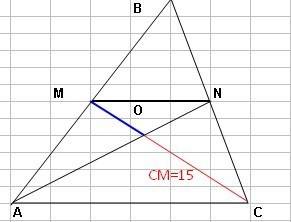
2. Начертим треугольник и увидим, что MN это средняя линия и значит равна половине основания => MN=0,5*AC , значит AC/MN=2
треугольники AOC и MNO подобны, т.к. все углы их равны. Из подобия напишем OC/MO = AC/MN = 2 значит OC=2MO, т.е. MO равна одной части из трех отрезка MC. Или MO = 1/3MC = 15/3 = 5
ответ MO = 5
1. Пусть скорость баржи x, тогда по течению она шла t=S/V со скоростью x+5 запишем => t₁=S₁/(x+5)=40/(x+5) , а против течения 30км со скоростью x-5 запишем => t₂=S₂/(x-5)=30/(x-5) и всего потратила 5 часов, значит
t₁ + t₂ = 5 подставим и решим 40/(x+5) + 30/(x-5) = 5 избавимся от дробей и решим квадратное уравнение 40*(x-5) + 30*(x+5) = 5*(x-5)*(x+5)
5*x² - 125 = 40x - 200 + 30x +150 перенесем влево и приведем подобные и разделим на 5
x² - 14x - 15 = 0 по теореме Виета находим корни 15 и -1, но скорость положительна и значит равна 15км/ч
ответ Скорость баржи 15 км/ч
23990 м ( приближенно равно) 23 км
24 км >20 км - истинное высказывание
850-98=752 ц
752 ц ( приближённо равно) 75 т
75 т > 50 т - истинное высказывание
1789+800=2589 мм
2589 мм ( приближённо равно) 260 см
260 см < 290 см - ложное высказывание.