3,5 см.
Пошаговое объяснение:
Используем формулу теоремы Пифагора для прямоугольного треугольника:
a ^ 2 + b ^ 2 = c ^ 2.
Диагональ фигуры в квадрате:
2 ^ 2 + 3 ^ 2 + 6 ^ 2 = 4 + 9 + 36 = 13 + 36 = 49.
Тогда диагональ прямоугольного параллелепипеда равна:
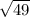 = 7 (см).
= 7 (см).
Зная, что длина диагонали прямоугольного параллелепипеда равна диаметру описанного шара / сферы, имеем:
D = 7 (см).
Из формулы:
D = 2 * R,
найдём радиус:
R = D / 2.
Подставим вычисленное значение диаметра в формулу:
R = 7 / 2 = 3,5 (см) - радиус описанного около прямоугольного параллелепипеда шара.
ответ: x∈[-2;4].
Пошаговое объяснение:
1) Составляем выражение для отношения a(n+1)/a(n), где a(n+1) и a(n) - соответственно n+1 - й и n - ный члены ряда: a(n+1)/a(n)=(x-1)*(3*n-1)²/[3*(3*n+2)²].
2) Составляем выражение для модуля этого отношения. Так как (3*n-1)²>0 и 3*(3*n+2)²>0, то /a(n+1)/a(n)/=/x-1/*(3*n-1)²/[3*(3*n+2)²].
3) Находим предел этого выражения при n⇒∞: lim /a(n+1)/a(n)/=1/3*/x-1/, так как lim (3*n-1)²/[3*(3*n+2)²]=1/3.
4) Составляем и решаем неравенство 1/3*/x-1/<1. Оно имеет решение -2<x<4, то есть x∈(-2;4). Поэтому -2<x<4 - интервал сходимости ряда.
5) Остаётся исследовать поведение ряда на концах этого интервала.
а) если x=-2, то ряд принимает вид (-1)^n/[(3*n-1)²]. Так как /(-1)^n/[(3*n-1)²]/=1/[(3*n-1)²]<1/n², а ряд обратных квадратов сходится, то в точке x=-2 данный ряд тоже сходится, причём - абсолютно.
б) если x=4, то ряд принимает вид 1/[(3*n-1)²]. Как только что было показано, данный ряд сходится - значит, данный ряд сходится и в этой точке. Поэтому областью сходимости ряда является интервал x∈[-2;4].
В - 52.890 = 28.360 : 40
В - 52.890 = 709
В = 709 + 52.890
В = 53.599
проверка:
28.360 : (53.599 - 52.890) = 40
28.360 : 709 = 40
40 = 40