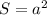Найди длину стороны квадрата периметр которого равен 8 см.вычесли его площадь

Question

Математика: Найди длину стороны квадрата периметр которого равен 8 см.вычесли его площадь

alenaafaunova · Accepted Answer

Так как

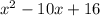находится под модулем, то знак этого трехчлена будет всегда (+), значит при определении промежутка решений неравенства его можно не учитывать, но так как неравенство строгое, то корни данного трехчлена не будут входить в промежуток решения.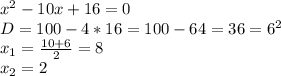
находим корни:
$x^2-10x+16=0 \\D=100-4*16=100-64=36=6^2 \\x_1= \frac{10+6}{2}=8 \\x_2=2$
теперь определяем x^3>0:
если x<0, то x^3<0
если x>0, то X^3>0
значит промежутком решения данного неравенства является:
x∈(0;2) и (2;8) и (8;+oo)
считаем на интервале (-1;7] неравенство верно при x=1; x=3; x=4; x=5; x=6; x=7 - всего 6 целых решений
ответ: 6 решений

MOGZ ответил